Question

已知≤a≤1,若f(x)=ax²-2x+1在［1,3］上的最大值为M（a），最小值为N(a),设g(a)=M（a）-N(a).

______________________________.（先在横线上填上一个结论，然后再解答）

Answer 1

构建问题：已知≤a≤1，若f(x)=ax²-2x+1在［1，3］上的最大值为M(a),最小值为N(a),设g(a)=M（a）-N(a).

判断函数g(a)的单调性，并求出g(a)的最小值.

解析：∵f(x)=a(x-)²+1-,

∴f(x)的图象为开口向上的抛物线.

∵1≤≤3,x∈［1,3］,

当x=时，f(x)有最小值N（a）=1-,f(1)=a-1,f(3)=9a-5,f(1)-f(3)=-8(a-).

当＜a≤1时，f(1)＜f(3),

∴M(a)=9a-5.

当≤a≤时，f(1)≥f(3),

∴M(a)=a-1.

∴g(a)=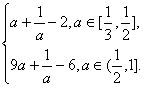

设≤a₁≤a₂≤,则g(a₁)-g(a₂)=(a₁-a₂)(1-)＞0,

∴g(a₁)＞g(a₂).

∴g(a)在［，］上是减函数.

同理，可证g(a)在（,1］上是增函数.

∴当a=时，g(a)有最小值.