
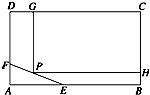
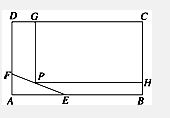
 如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.
如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.| EN |
| 40 |
| x-140 |
| 60 |
| 2x-280 |
| 3 |
| 760-2x |
| 3 |
| 1 |
| 6 |
| EN |
| 40 |
| x-140 |
| 60 |
| 2x-280 |
| 3 |
| 2x-280 |
| 3 |
| 760-2x |
| 3 |
| 1 |
| 6 |
| 760 |
| 2 |
| 72200 |
| 3 |
| 72200 |
| 3 |


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
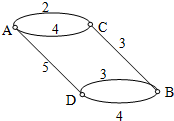 如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )
如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )| A、11 | B、10 | C、8 | D、7 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| n(12-an) |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com