
 ,其中向量
,其中向量 =(cos
=(cos ,sin
,sin ) (x∈R),向量
) (x∈R),向量 =(cos?,sin?)(|?|<
=(cos?,sin?)(|?|< ),f(x)的图象关于直线x=
),f(x)的图象关于直线x= 对称.
对称. 的图象按向量
的图象按向量 =(m,n) (|m|<π)平移可得到函数y=f(x)的图象,求向量
=(m,n) (|m|<π)平移可得到函数y=f(x)的图象,求向量 .
. =cos
=cos cos?+sin
cos?+sin sin?=cos(
sin?=cos( -?),
-?), 对称,
对称,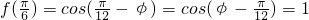 ,
,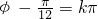 ,k∈Z,又|?|<
,k∈Z,又|?|< ,∴?=
,∴?= .
. -
- )=sin(
)=sin( +
+ )=sin
)=sin (x+
(x+ ),
), 平移到y=sin
平移到y=sin (x+
(x+ ),只需向左平移
),只需向左平移 单位,
单位, =(m,n) (|m|<π),
=(m,n) (|m|<π),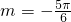 ,n=-1,即
,n=-1,即 =(-
=(- ,-1).
,-1). -
- )=sin(
)=sin( +
+ )=sin
)=sin (x+
(x+ ),
),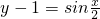 平移到
平移到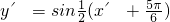 ,只要
,只要 即
即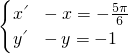 ,
, =(-
=(- ,-1).
,-1). 的图象按向量
的图象按向量 =(m,n) (|m|<π)平移,求出函数的解析式,利用与函数y=f(x)的图象相同,求向量
=(m,n) (|m|<π)平移,求出函数的解析式,利用与函数y=f(x)的图象相同,求向量 .另解:通过函数y=f(x)逆向推出函数,使得与函数y=1+sin
.另解:通过函数y=f(x)逆向推出函数,使得与函数y=1+sin 的图象相同,求出向量
的图象相同,求出向量 .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2007年江苏省苏锡常镇四市高考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com