
如图,圆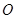 与离心率为
与离心率为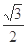 的椭圆
的椭圆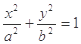 (
(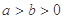 )相切于点
)相切于点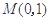 .
.
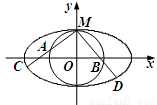
(Ⅰ)求椭圆的方程;
(Ⅱ)过点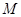 引两条互相垂直的两直线
引两条互相垂直的两直线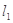 、
、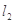 与两曲线分别交于点
与两曲线分别交于点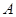 、
、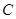 与点
与点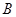 、
、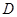 (均不重合).
(均不重合).
(ⅰ)若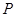 为椭圆上任一点,记点
为椭圆上任一点,记点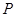 到两直线的距离分别为
到两直线的距离分别为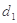 、
、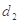 ,求
,求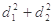 的最大值;
的最大值;
(ⅱ)若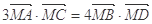 ,求
,求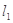 与
与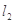 的方程.
的方程.
(Ⅰ)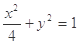 。
。
(Ⅱ) 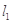 的方程为
的方程为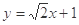 ,
,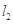 的方程为
的方程为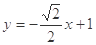
或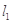 的方程为
的方程为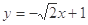 ,
,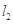 的方程为
的方程为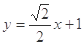 。
。
【解析】
试题分析:(Ⅰ)由题意: 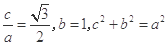 解得
解得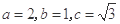 2分
2分
椭圆的方程为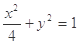 3分
3分
(Ⅱ)(ⅰ)设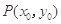 因为
因为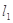 ⊥
⊥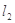 ,则
,则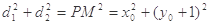 因为
因为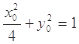
所以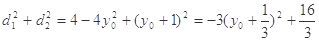 5分
5分
因为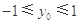
所以当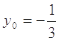 时
时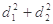 取得最大值为
取得最大值为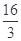 ,此时点
,此时点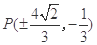 6分
6分
(ⅱ)设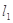 的方程为
的方程为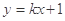 ,由
,由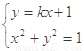 解得
解得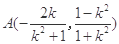
由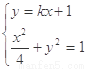 解得
解得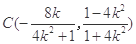 8分
8分
同理可得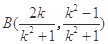 ,
,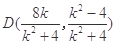 10分
10分
所以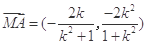 ,
,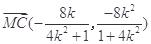
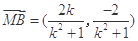 ,
,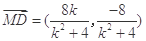
由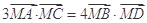 得
得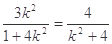 解得
解得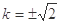 13分
13分
所以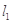 的方程为
的方程为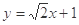 ,
,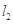 的方程为
的方程为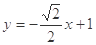
或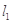 的方程为
的方程为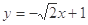 ,
,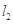 的方程为
的方程为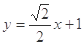 14分
14分
考点:本题主要考椭圆的标准方程,椭圆的几何性质,直线椭圆的位置关系,圆的切线。
点评:难题,求椭圆的标准方程,主要运用了椭圆的几何性质,a,b,c,e的关系。曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题(2)结合向量的坐标运算,确定得到k的方程,为进一步确定直线方程奠定基础。


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
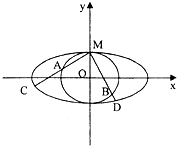 (2013•东莞二模)如图,圆O与离心率为
(2013•东莞二模)如图,圆O与离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| d | 2 1 |
| d | 2 2 |
| MA |
| MC |
| MB |
| MD |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏苏州高级中学高三12月月考数学试卷(解析版) 题型:解答题
如图,圆O与离心率为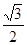 的椭圆T:
的椭圆T: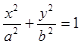 (
(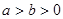 )相切于点M
)相切于点M 。
。
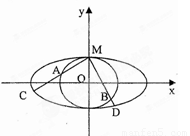
⑴求椭圆T与圆O的方程;
⑵过点M引两条互相垂直的两直线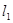 、
、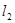 与两曲线分别交于点A、C与点B、D(均不重合)。
与两曲线分别交于点A、C与点B、D(均不重合)。
①若P为椭圆上任一点,记点P到两直线的距离分别为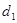 、
、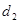 ,求
,求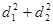 的最大值;
的最大值;
②若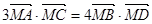 ,求
,求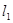 与
与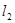 的方程。
的方程。
查看答案和解析>>
科目:高中数学 来源:2013年江苏省盐城市高考数学二模试卷(解析版) 题型:解答题
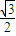 的椭圆T:
的椭圆T: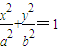 (a>b>0)相切于点M(0,1).
(a>b>0)相切于点M(0,1).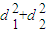 的最大值;
的最大值;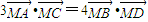 ,求l1与l2的方程.
,求l1与l2的方程.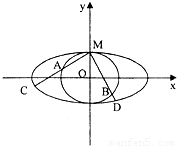
查看答案和解析>>
科目:高中数学 来源:2013年广东省东莞市高考数学二模试卷(文科)(解析版) 题型:解答题
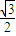 的椭圆T:
的椭圆T: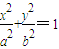 (a>b>0)相切于点M(0,1).
(a>b>0)相切于点M(0,1).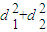 的最大值;
的最大值;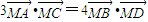 ,求l1与l2的方程.
,求l1与l2的方程.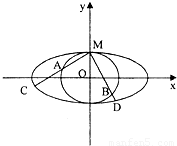
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com