
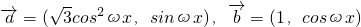 (其中ω>0),已知
(其中ω>0),已知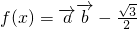 且f(x)最小正周期为2π
且f(x)最小正周期为2π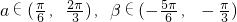 ,
,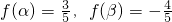 求cos(α-β)的值.
求cos(α-β)的值.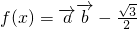 =
= cos2ωx+sinωx•cosωx-
cos2ωx+sinωx•cosωx- =
= sin2ωx+
sin2ωx+ cosωx=sin(2ωx+
cosωx=sin(2ωx+ ).
).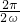 =2π,ω=
=2π,ω= ,
, ).
). ,∴sin(α+
,∴sin(α+ )=
)= .
. ,
, ),∴α+
),∴α+ ∈(
∈( ,π),cos(α+
,π),cos(α+ )=-
)=- .
. ,可得sin(β+
,可得sin(β+ )=-
)=- .再由β∈(-
.再由β∈(- ,-
,- ),可得β+
),可得β+ ∈(-
∈(- ,0),
,0), )=
)= .
. )-(β+
)-(β+ )]=cos(α+
)]=cos(α+ )cos(β+
)cos(β+ )-sin(α+
)-sin(α+ )•sin(β+
)•sin(β+ )=(-
)=(- )•(
)•(  )+(
)+(  )•(-
)•(- )=-
)=- .
.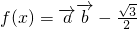 的解析式为 sin(2ωx+
的解析式为 sin(2ωx+ ),再由ω>0,T=
),再由ω>0,T=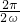 =2π,求得ω的值,即可求得f(x)的解析式.
=2π,求得ω的值,即可求得f(x)的解析式. )、cos(β+
)、cos(β+ ),由cos(α-β)=cos[(α+
),由cos(α-β)=cos[(α+ )-(β+
)-(β+ )]利用两角和差的余弦公式求出结果.
)]利用两角和差的余弦公式求出结果.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 9r2 |
| 4 |
| PQ |
| QN |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a(x-1) | x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:增城市2007届华侨中学高三四月份月考试题\数学(理科) 题型:044
已知函数.f(x)=2x3+ax与g(x)=bx2+cx的图象都过点P(2,0),且在点P处有公共切线.
(1)求f(x)和g(x)的表达式及在点P处的公切线方程;
(2)设![]() ,其中m<0,求F(x)的单调区间.
,其中m<0,求F(x)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com