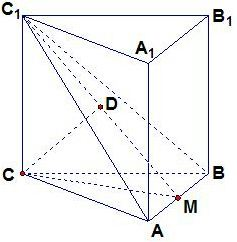
分析:在立体几何中,求点到平面的距离是一个常见的题型,同时求直线到平面的距离、平行平面间的距离及多面体的体积也常转化为求点到平面的距离.本题采用的是“找垂面法”:即找(作)出一个过该点的平面与已知平面垂直,然后过该点作其交线的垂线,则得点到平面的垂线段.观察点的位置可知:点B1到平面ABC1的距离就等于点C到平面ABC1的距离,取AB得中点M,连接CM,C1M,过点C作CD⊥C1M,垂足为D,则平面ABC1⊥平面C1CM,所以CD⊥平面C1AB,故CD的长度即为点C到平面ABC1的距离,在Rt△C1CM中,利用等面积法即可求出CD的长度.
解答:解:如图所示,取AB得中点M,连接CM,C
1M,过点C作CD⊥C
1M,垂足为D
∵C
1A=C
1B,M为AB中点,
∴C
1M⊥AB
∵CA=CB,M为AB中点,
∴CM⊥AB
又∵C
1M∩CM=M,
∴AB⊥平面C
1CM
又∵AB?平面ABC
1,
∴平面ABC
1⊥平面C
1CM,平面ABC
1∩平面C
1CM=C
1M,CD⊥C
1M,
∴CD⊥平面C
1AB,
∴CD的长度即为点C到平面ABC
1的距离,即点B
1到平面ABC
1的距离
在Rt△C
1CM中,C
1C=1,CM=
,C
1M=
∴CD=
,即点B
1到平面ABC
1的距离为
故答案为:
点评:本小题主要考查棱柱,线面关系、点到平面的距离等基本知识,同时考查空间想象能力和推理、运算能力.




 如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( )
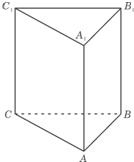
如图,在正三棱柱ABC-A1B1C1中,AB=1,若二面角C-AB-C1的大小为60°,则点C到平面C1AB的距离为( ) 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2. 如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1B1C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= (2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.
(2012•马鞍山二模)如图,在正三棱柱ABC一DEF中,AB=2,AD=1,P是CF的延长线上一点,过A、B、P三点的平面交FD于M,交EF于N.