
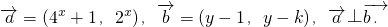
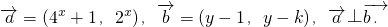
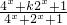 ;
;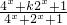 =1+
=1+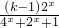
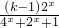 的最小值为-4
的最小值为-4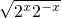 +1=3
+1=3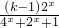 =
=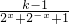 ≤
≤ ;当k<1时,
;当k<1时,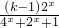 =
=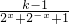 ≥
≥ ;
; =-4,解之得k=-11
=-4,解之得k=-11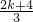 且1<f(x3)≤
且1<f(x3)≤ ,
, ≤2,解之得1<k≤4;
≤2,解之得1<k≤4;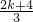 ≤f(x1)+f(x2)<2,且
≤f(x1)+f(x2)<2,且 ≤f(x3)<1,
≤f(x3)<1,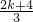 ≥1,解之得-
≥1,解之得- ≤k<1;
≤k<1; ,4]
,4]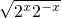 +1=3.再根据k与1的大小关系分类讨论,即可得到必定有k<1,且当2x=2-x=1即x=0时,函数有最小值为-3,由此解关于k的等式即得实数k的值.
+1=3.再根据k与1的大小关系分类讨论,即可得到必定有k<1,且当2x=2-x=1即x=0时,函数有最小值为-3,由此解关于k的等式即得实数k的值.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:高中数学 来源:2012-2013学年湖北省黄冈市罗田县育英高中高一(上)期末数学试卷(解析版) 题型:解答题
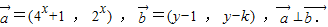
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量![]()
(1)求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数![]() 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的![]() ,把所得到的图象再向左平移
,把所得到的图象再向左平移![]() 单位,得到函数
单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com