
【题目】观察以下等式:
13=12
13+23=(1+2)2
13+23+33=(1+2+3)2
13+23+33+43=(1+2+3+4)2
(1)请用含n的等式归纳猜想出一般性结论,并用数学归纳法加以证明.
(2)设数列{an}的前n项和为Sn,且an=n3+n,求S10.
【答案】(1)猜想13+23+33+…+n3=(1+2+3+…+n)2;证明见解析(2)3080
【解析】
(1)根据式子猜想出一般性结论,然后当![]() 时,证明成立,假设
时,证明成立,假设![]() 时,式子也成立,然后对
时,式子也成立,然后对![]() 时的式子进行化简,从而证明结论成立;(2)对
时的式子进行化简,从而证明结论成立;(2)对![]() 进行分组求和,然后根据(1)中所得到的求和公式,进行求和计算,得到答案.
进行分组求和,然后根据(1)中所得到的求和公式,进行求和计算,得到答案.
(1)猜想13+23+33+…+n3=(1+2+3+…+n)2;
证明:当n=1时,左边=1,右边=1,等式成立;
假设n=k时,13+23+33+…+k3=(1+2+3+…+k)2,
当n=k+1时,13+23+33+…+k3+(k+1)3=(1+2+3+…+k)2+(k+1)3
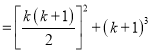
![]()
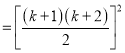
![]() ,
,
可得n=k+1时,猜想也成立,
综上可得对任意的正整数n,13+23+33+…+n3=(1+2+3+…+n)2;
(2)数列{an}的前n项和为Sn,且an=n3+n,
S10=(13+23+…+103)+(1+2+3+…+10)=(1+2+…+10)2![]()
=552+55=3080.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】![]() 是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国
是指大气中空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国![]() 标准采用世界卫生组织设定的最宽限值,即
标准采用世界卫生组织设定的最宽限值,即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标.某城市环保局从该市市区2017年上半年每天的![]() 监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).
监测数据中随机抽取18天的数据作为样本,将监测值绘制成茎叶图如下图所示(十位为茎,个位为叶).

(1)求这18个数据中不超标数据的平均数与方差;
(2)在空气质量为一级的数据中,随机抽取2个数据,求其中恰有一个为![]() 日均值小于30微克/立方米的数据的概率;
日均值小于30微克/立方米的数据的概率;
(3)以这![]() 天的
天的![]() 日均值来估计一年的空气质量情况,则一年(按
日均值来估计一年的空气质量情况,则一年(按![]() 天计算)中约有多少天的空气质量超标.
天计算)中约有多少天的空气质量超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
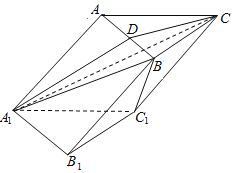
【题目】如图,在底边为等边三角形的斜三棱柱ABC﹣A1B1C1中,AA1![]() AB,四边形B1C1CB为矩形,过A1C作与直线BC1平行的平面A1CD交AB于点D.
AB,四边形B1C1CB为矩形,过A1C作与直线BC1平行的平面A1CD交AB于点D.
(Ⅰ)证明:CD⊥AB;
(Ⅱ)若AA1与底面A1B1C1所成角为60°,求二面角B﹣A1C﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,且倾斜角为
,且倾斜角为![]() ,在极坐标系(与平面直角坐标系
,在极坐标系(与平面直角坐标系![]() 取相同的长度,以原点
取相同的长度,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴)中,曲线
轴的非负半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的参数方程与曲线
的参数方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示:
的部分图象如图所示:
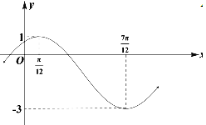
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的单调区间和对称中心坐标;
的单调区间和对称中心坐标;
(3)将![]() 的图象向左平移
的图象向左平移![]() 个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数
个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装公司生产得到衬衫,每件定价80元,在某城市年销售8万件,现在该公司在该市设立代理商来销售衬衫代理商要收取代销费,代销费为销售金额的![]() %(即每销售100元收取
%(即每销售100元收取![]() 元),为此,该衬衫每件价格要提高到
元),为此,该衬衫每件价格要提高到![]() 元才能保证公司利润.由于提价每年将少销售
元才能保证公司利润.由于提价每年将少销售![]() 万件,如果代理商每年收取的代销费不小于16万元,则
万件,如果代理商每年收取的代销费不小于16万元,则![]() 的取值范围是___________
的取值范围是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足
满足![]() 且
且![]() ,则称函数
,则称函数![]() 为“
为“![]() 函数”.
函数”.
![]() 试判断
试判断![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
![]() 函数
函数![]() 为“
为“![]() 函数”,且当
函数”,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并写出在
的解析式,并写出在![]() 上的单调递增区间;
上的单调递增区间;
![]() 在
在![]() 条件下,当
条件下,当![]() 时,关于
时,关于![]() 的方程
的方程![]() 为常数
为常数![]() 有解,记该方程所有解的和为
有解,记该方程所有解的和为![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com