


 的实数m,n.
的实数m,n. 满足
满足 ,且
,且 求
求 .
.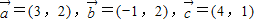 ,我们易求出
,我们易求出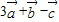 的坐标,代入向量模的公式,即可得到答案.
的坐标,代入向量模的公式,即可得到答案.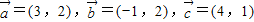 及
及 ,我们可构造一个关于m,n的方程组,解方程组,即可得到实数m,n的值.
,我们可构造一个关于m,n的方程组,解方程组,即可得到实数m,n的值.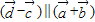 ,由向量的共线定理,我们易得
,由向量的共线定理,我们易得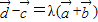 ,又由
,又由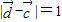 ,我们可以得到一个关于λ的方程,解方程求出λ的值,进而求以求出向量
,我们可以得到一个关于λ的方程,解方程求出λ的值,进而求以求出向量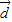 的坐标.
的坐标. =(4,7)(3分)
=(4,7)(3分)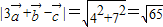 (5分)
(5分)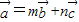 得
得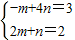 (8分)
(8分)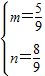 (10分)
(10分)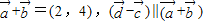
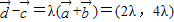 (λ∈R)(11分)
(λ∈R)(11分)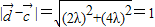 ∴
∴ (14分)
(14分) ,(15分)
,(15分)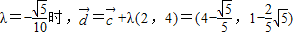 .(16分)
.(16分)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com