
已知函数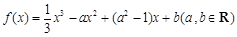
⑴若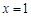 为
为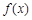 的极值点,求
的极值点,求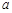 的值;
的值;
⑵若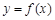 的图象在点
的图象在点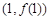 处的切线方程为
处的切线方程为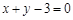 ,求
,求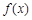 在区间
在区间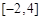 上的最大值;
上的最大值;
⑶当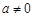 时,若
时,若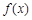 在区间
在区间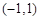 上不单调,求
上不单调,求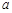 的取值范围.
的取值范围.
⑴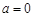 或2.⑵
或2.⑵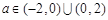 .
.
【解析】
试题分析:⑴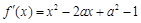 ,∵
,∵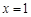 是
是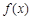 的极值点,∴
的极值点,∴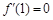 ,即
,即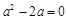 ,解得
,解得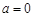 或2.
或2.
⑵∵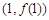 在
在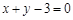 上.∴
上.∴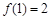 ,∵
,∵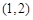 在
在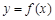 上,∴
上,∴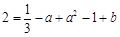 ,又
,又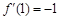 ,∴
,∴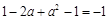 ,∴
,∴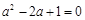 ,解得
,解得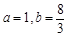 ,∴
,∴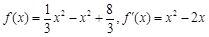 ,由
,由 可知
可知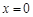 和
和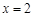 是
是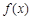 的极值点.∵
的极值点.∵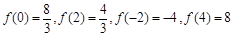 ,∴
,∴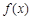 在区间
在区间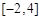 上的最大值为8.
上的最大值为8.
⑶因为函数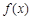 在区间
在区间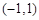 不单调,所以函数
不单调,所以函数 在
在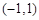 上存在零点.而
上存在零点.而 的两根为
的两根为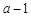 ,
,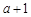 ,区间长为
,区间长为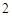 ,∴在区间
,∴在区间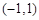 上不可能有2个零点.所以
上不可能有2个零点.所以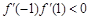 ,即
,即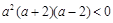 .∵
.∵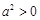 ,∴
,∴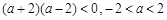 .又∵
.又∵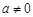 ,∴
,∴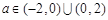 .
.
考点:本题主要考查导数计算及其几何意义,应用导数研究函数的最值。
点评:典型题,在给定区间,导数值非负,函数是增函数,导数值为非正,函数为减函数。求极值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值、计算得到函数值比较大小。切线的斜率为函数在切点的导数值。(3)将条件转化成函数 在
在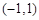 上存在零点,体现了转化与化归思想的应用。
上存在零点,体现了转化与化归思想的应用。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
(08年威海市质检文) (14分)
已知函数![]() 在点
在点![]() 处取得极小值-4,使其导数
处取得极小值-4,使其导数![]() 的
的![]() 的取值范围为
的取值范围为![]() ,求:
,求:
(1)![]() 的解析式;
的解析式;
(2)若过点![]() 可作曲线
可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011届北京市西城区高三二模考试理科数学 题型:解答题
((本小题满分14分)
已知函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当 时,求曲线
时,求曲线 在
在 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积;
(Ⅱ)若函数 存在一个极大值点和一个极小值点,且极大值与极小值的积为
存在一个极大值点和一个极小值点,且极大值与极小值的积为 ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2011届江西省临川二中高三第二学期第一次模拟考试理科数学 题型:解答题
(本小题满分14分)
已知函数 ,当
,当 时,
时, 取得极
取得极 小值
小值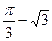 .
.
(1)求 ,
, 的值;
的值;
(2)设直线 ,曲线
,曲线 .若直线
.若直线
 与曲线
与曲线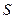 同时满足下列两个条件:
同时满足下列两个条件:
①直线 与曲线
与曲线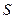 相切且至少有两个
相切且至少有两个 切点;
切点;
②对任意 都有
都有 .则称直线
.则称直线 为曲线
为曲线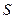 的“上夹线”.
的“上夹线”.
试证明:直线 是曲线
是曲线 的“上夹线”.
的“上夹线”.
(3)记 ,设
,设 是方程
是方程 的实数
的实数 根,若对于
根,若对于 定义域中任意的
定义域中任意的 、
、 ,当
,当 ,且
,且 时,问是否存在一个最小的正整数
时,问是否存在一个最小的正整数 ,使得
,使得 恒成立,若存在请求出
恒成立,若存在请求出 的值;若不存在请说明理由.
的值;若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届江西南昌10所省重点中学高三第二次模拟突破冲刺理科数学(一)(带解析) 题型:填空题
A.(不等式选讲)已知函数 .若关于x的不等式
.若关于x的不等式 的解集是
的解集是 ,则的取值范围是
,则的取值范围是
B.(坐标系与参数方程选做题)在极坐标系中,已知曲线 与直线
与直线 相切,则实数
相切,则实数 的值为_______
的值为_______
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟突破冲刺理科数学(一)(解析版) 题型:填空题
A.(不等式选讲)已知函数 .若关于x的不等式
.若关于x的不等式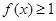 的解集是
的解集是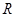 ,则的取值范围是
,则的取值范围是
B.(坐标系与参数方程选做题)在极坐标系中,已知曲线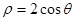 与直线
与直线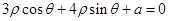 相切,则实数
相切,则实数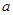 的值为_______
的值为_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com