
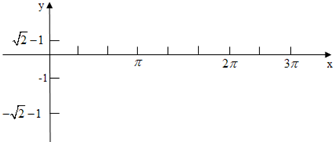
分析 (1)依题意可得A,B,T的值,利用周期公式可求$ω=\frac{2π}{4π}=\frac{1}{2}$,又$sin(\frac{1}{2}×\frac{π}{3}+φ)=1$,结合范围|φ|<$\frac{π}{2}$,
可求φ的值,从而可求函数解析式.
(2)列表描点连线,由五点法即可作函数y=Asin(ωx+φ)的图象.
解答 解:(1)依题意:$A=\sqrt{2},B=-1,T=2(\frac{7π}{3}-\frac{π}{3})=4π$,
∴$ω=\frac{2π}{4π}=\frac{1}{2}$,
∴$y=\sqrt{2}sin(\frac{x}{2}+φ)-1$,又$sin(\frac{1}{2}×\frac{π}{3}+φ)=1$,
∴$\frac{π}{6}+φ=k+\frac{π}{2}{\;}^{\;}(k∈Z){\;}^{\;}∴φ=kπ+\frac{π}{3},又|φ|<\frac{π}{2},(k∈Z)$,
∴$φ=\frac{π}{3}$,
∴$y=\sqrt{2}sin(\frac{x}{2}+\frac{π}{3})-1$
(2)列表如下:
| x | 0 | $\frac{π}{3}$ | $\frac{4π}{3}$ | $\frac{7π}{3}$ | 3π |
| $\frac{x}{2}+\frac{π}{3}$ | $\frac{π}{3}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | $\frac{11π}{6}$ |
| $y=\sqrt{2}sin(\frac{Χ}{2}+\frac{π}{3})-1$ | $\frac{{\sqrt{6}}}{2}-1$ | $\sqrt{2}-1$ | -1 | $-\sqrt{2}-1$ | $-\frac{{\sqrt{2}}}{2}-1$ |

点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象,属于中档题.


科目:高中数学 来源: 题型:填空题
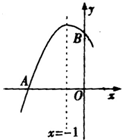 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),B(0,3),对称轴为x=-1,给出下面四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com