
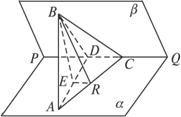
(1)求证:AB⊥PQ;
(2)求点B到平面α的距离;
(3)设R是线段CA上的一点,直线BR与平面α所成的角为45°,求线段CR的长度.
(1)证明:在平面β内作BD⊥PQ于D,连结AD.
∵∠ACP=∠BCP=30°,CA=CB=a,CD公用,
∴△ACD≌△BCD.
∴∠ADC=∠BDC=90°,即AD⊥PQ.
于是PQ⊥平面ABD,则AB⊥PQ.
(2)解:由(1)知∠ADB是二面角α-PQ-β的平面角,
∴∠ADB=60°.又PQ⊥平面ABD,
∴α⊥平面ABD.
过B作BE⊥AD于点E,则BE即为B到平面α的距离.
BE=BD·sin60°=BC·sin30°·sin60°=![]() a.
a.
(3)解:连结ER,
∵BE⊥α,
∴∠BRE是BR与α所成的角,
即∠BRE=45°,则有BR=![]() =
=![]() a.
a.
易知△ABD为正三角形,AB=AD=BD=![]() a.
a.
在△ABC中,由余弦定理得cos∠BCA=![]() .
.
在△BCR中,设CR=x,由余弦定理得(![]() a)2=x2+a2-2ax·
a)2=x2+a2-2ax·![]() ,求得x1=
,求得x1=![]() ,x2=
,x2=![]() (舍去,∵CR<AC=a),故CR=
(舍去,∵CR<AC=a),故CR=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,已知二面角α-AB-β的大小为120°,PC⊥α于C,PD⊥β于D,且PC=2,PD=3.
如图,已知二面角α-AB-β的大小为120°,PC⊥α于C,PD⊥β于D,且PC=2,PD=3.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•成都三模)如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( )
(2008•成都三模)如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( )查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.
如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.查看答案和解析>>
科目:高中数学 来源:2014届四川省攀枝花市高二上学期期中理科数学试卷(解析版) 题型:选择题
如图,已知二面角α-PQ-β的大小为60°,点C为棱PQ上一点,A∈β,AC=2,∠ACP=30°,则点A到平面α的距离为( )

A.1 B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com