C
分析：根据题意知道贷款a万元，年利率为q，按复利计算5年后的本息和为a（1+q）
5万元；设每年偿还x万元，第一年底偿还x万元的本息和为x（1+q）
4，第二年底偿还x万元的本息和为x（1+q）
3，第三年底偿还x万元的本息和为x（1+q）
2，第四年底偿还x万元的本息和为x（1+q），第五年底偿还x万元全部还清，一共还了[x（1+q）
4+x（1+q）
3+x（1+q）
2+x（1+q）+x]万元，则[x（1+q）
4+x（1+q）
3+x（1+q）
2+x（1+q）+x]=a（1+q）
5，算出x即可．
解答：由题意知：
∵贷款a万元，年利率为q，按复利计算
∴5年后的本息和为a（1+q）
5万元
设每年偿还x万元，则：
第一年底偿还x万元的本息和为x（1+q）
4万元，
第二年底偿还x万元的本息和为x（1+q）
3万元，
第三年底偿还x万元的本息和为x（1+q）
2万元，
第四年底偿还x万元的本息和为x（1+q）万元，
第五年底偿还x万元
即：五年一共偿还[x（1+q）
4+x（1+q）
3+x（1+q）
2+x（1+q）+x]万元
相当于贷款a万元，年利率为q，按复利计算5年后的本息和为a（1+q）
5万元
∴[x（1+q）
4+x（1+q）
3+x（1+q）
2+x（1+q）+x]=a（1+q）
5根据，
∴x=
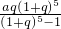
万元．
故选C．
点评：本题主要考查数列的实际应用问题，现实生活中得房贷的复利计算，对等比数列前n项和公式的计算能力要求较高．综合性强，难度大，容易出错．
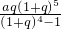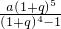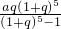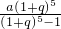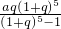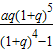万元
万元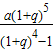
万元
万元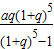
万元
万元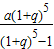
万元
万元