
(附加题,10分)已知函数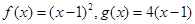 ,数列
,数列 满足
满足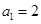 ,且
,且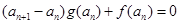 .
.
(1)试探究数列 是否是等比数列?(5分)
是否是等比数列?(5分)
(2)试证明 .(5分)
.(5分)
(1)数列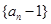 是首项为
是首项为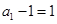 ,公比为
,公比为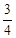 的等比数列. (2)证明:见解析。
的等比数列. (2)证明:见解析。
【解析】本试题主要是考查了等比数列的定义和运用数列的求和证明不等式的运用。
(1)由已知的关系式化简变形得到数列的递推关系,然后分析证明得到。
(2)由(1)知数列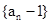 是首项为1,公比为
是首项为1,公比为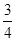 的等比数列
的等比数列
得到通项公式,进而分析求和,得到证明。
解:(1)由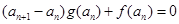 得
得
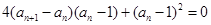 ,即
,即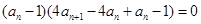 ----------1分
----------1分
∴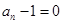 或
或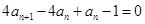 ∵
∵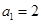 ,∴
,∴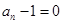 不合舍去.
不合舍去.
由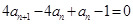 得
得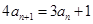 ,
, ,(
,(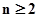 )--------3分
)--------3分
∴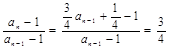 ,
,
∴数列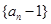 是首项为
是首项为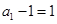 ,公比为
,公比为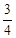 的等比数列. -------------------5分
的等比数列. -------------------5分
(2)证明:由(1)知数列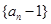 是首项为
是首项为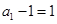 ,公比为
,公比为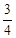 的等比数列
的等比数列
∴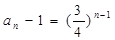 ,∴
,∴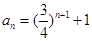 , ------------------6分
, ------------------6分
∴ =
=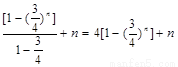 ---8分
---8分
∵对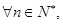 有
有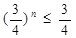 ,
,
∴ ,∴
,∴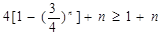 ,即
,即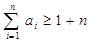 ---10分
---10分


 每课必练系列答案
每课必练系列答案科目:高中数学 来源:2015届广东省高一上学期期中考试数学试卷(解析版) 题型:解答题
(附加题)本小题满分10分
已知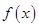 是定义在
是定义在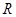 上单调函数,对任意实数
上单调函数,对任意实数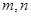 有:
有: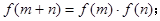 且
且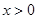 时,
时,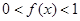 .
.
(1)证明: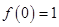 ;
;
(2)证明:当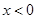 时,
时,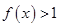 ;
;
(3)当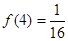 时,求使
时,求使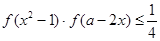 对任意实数
对任意实数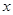 恒成立的参数
恒成立的参数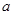 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届浙江省杭州市高一第一学期阶段考试数学 题型:解答题
附加题:本大题共2小题,每小题10分,共20分。
(本题满分10分)已知函数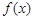 在
在 上为增函数,且f(
上为增函数,且f( )=
)= ,f(1)=2,集合
,f(1)=2,集合 ,关于
,关于 的不等式
的不等式 的解集为
的解集为 ,求使
,求使 的实数
的实数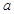 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010年甘肃省高二第二阶段考试数学理卷 题型:解答题
(本小题满分12分)已知椭圆C: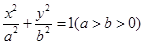 的离心率
的离心率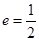 ,且原点
,且原点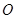 到直线
到直线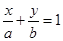 的距离为
的距离为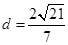 .
.
(Ⅰ)求椭圆的方程 ;
(Ⅱ)过点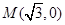 作直线与椭圆C交于
作直线与椭圆C交于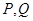 两点,求
两点,求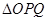 面积的最大值.
面积的最大值.
四.附加题 (共20分,每小题10分)
查看答案和解析>>
科目:高中数学 来源:2010-2011年浙江省杭州市高二下学期期中考试文数 题型:解答题
四、附加题:本大题共2小题,每小题10分,共20分。
(20)(本小题满分10分)
已知 是边长为1的正方形,
是边长为1的正方形,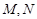 分别为
分别为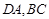 上的点,且
上的点,且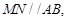 沿
沿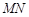 将正方形折成直二面角
将正方形折成直二面角 .
.
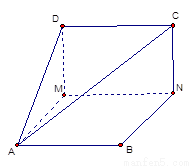
(I)求证:平面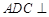 平面
平面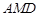 ;
;
(II)设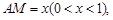 点
点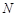 与平面
与平面 间的距离为
间的距离为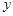 ,试用
,试用 表示
表示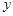 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com