
 函数
函数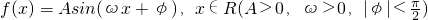 的一段图象如图5所示:将y=f(x)的图象向右平移m(m>0)个单位,可得到函数y=g(x)的图象,且图象关于原点对称,
的一段图象如图5所示:将y=f(x)的图象向右平移m(m>0)个单位,可得到函数y=g(x)的图象,且图象关于原点对称,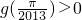 .
.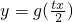 在区间
在区间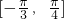 上最小值为-2,求实数t的取值范围.
上最小值为-2,求实数t的取值范围. =
= +
+ ,解得ω=2.
,解得ω=2. )+φ=0,解得 φ=
)+φ=0,解得 φ= .
. ,且g(x)=2sin2x.
,且g(x)=2sin2x.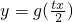 =2sintx (t≠0),当t>0时,由x在区间
=2sintx (t≠0),当t>0时,由x在区间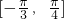 上,结合图象可得
上,结合图象可得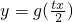 =2sintx 的周期为
=2sintx 的周期为  ,且满足-
,且满足- •
• ≥-
≥- ,即
,即  ≤
≤ ,故 t≥
,故 t≥ .
.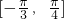 上,结合图象可得
上,结合图象可得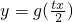 =2sintx 的周期为
=2sintx 的周期为  ,且满足
,且满足  •
• ≤
≤ ,即
,即  ≤π,t≤-2.
≤π,t≤-2. .
. ,故g(x)=2sin2x.
,故g(x)=2sin2x.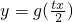 =2sintx 的周期为
=2sintx 的周期为  ,当t>0时,结合图象可得-
,当t>0时,结合图象可得- •
• ≥-
≥- ,由此求得t的范围.当t<0时,由x在区间
,由此求得t的范围.当t<0时,由x在区间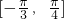 上,结合图象可得
上,结合图象可得  •
• ≤
≤ ,由此求得t的范围.再把以上求得的t的范围取并集,即得所求.
,由此求得t的范围.再把以上求得的t的范围取并集,即得所求.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 函数f(x)=Asin(ωx+φ),x∈R(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ),x∈R(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 2013 |
| tx |
| 2 |
| π |
| 3 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省常州市部分学校高二(下)期末数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com