
 ,且由此增加的产值分别为60万元、40万元、20万元、-5万元.设该企业当年因改造而增加利润为ξ.
,且由此增加的产值分别为60万元、40万元、20万元、-5万元.设该企业当年因改造而增加利润为ξ.| 评价得分 | (0,60) | 【60,70) | 【70,80) | 【80,100】 |
| 评价等级 | 不合格 | 合格 | 良好 | 优秀 |
| 奖惩 (万元) | -80 | 30 | 60 | 100 |
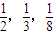 ,故易得到该企业能被抽到且被评为合格及其以上等次的概率.
,故易得到该企业能被抽到且被评为合格及其以上等次的概率.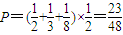
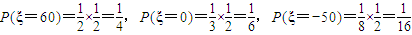
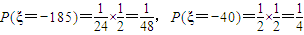 ,
,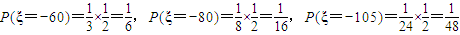
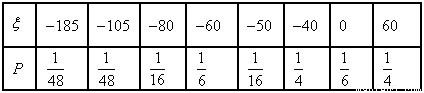
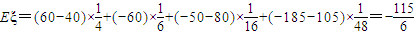 (万元)
(万元)

 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 8 |
| 1 |
| 24 |
| 评价得分 | (0,60) | [60,70) | [70,80) | [80,100] |
| 评价等级 | 不合格 | 合格 | 良好 | 优秀 |
| 奖惩 (万元) |
-80 | 30 | 60 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com