
分析 (1)根据等差数列的定义求出公差d=2,再求出首项,即可求出bn,
(2)根据裂项求和即可求出答案.
解答 解:(1)等差数列{an}中,a2=3,a4=7,
∴a4=a2+2d,
∴7=3+2d,
解得d=2,
∴a1=a2-d=1,
∴bn=a2n=1+2(2n-1)=4n-1,
(2)由(1)可得an=1+2(n-1)=2n-1,
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
∴$\{\frac{1}{{{a_n}{a_{n+1}}}}\}$的前n项和为$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$.
点评 本题考查了等差数列的通项公式和裂项求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 266,14 | B. | 256,14 | C. | 256,-$\frac{21}{4}$ | D. | 266,-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -1 | C. | 2或-1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
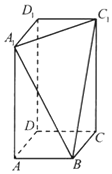 长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$
长方体ABCD-A1B1C1D1中,AB=BC=2,过A1,C1,B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,这个几何体的体积为$\frac{40}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{1}{2},\frac{1}{e}}]$ | B. | $({0,\frac{2}{e}}]$ | C. | $({-∞,0})∪[{\frac{2}{e},+∞})$ | D. | $({-∞,-\frac{1}{2}})∪[{\frac{1}{e},+∞})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com