
 , 若目标函数z=ax+by(a>0,b>0)的最大值为40,则
, 若目标函数z=ax+by(a>0,b>0)的最大值为40,则 的最小值为( )
的最小值为( ) A. | B.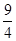 | C.1 | D.4 |
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:高中数学 来源:不详 题型:解答题
 元/分钟和200元/分钟,甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
元/分钟和200元/分钟,甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
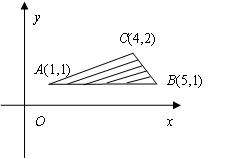
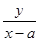 的最大值是 ( )
的最大值是 ( )| A.2 | B. | C.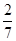 | D.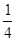 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
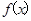 为奇函数,
为奇函数,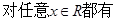
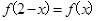 ,当
,当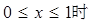
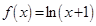 .若
.若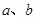 为正的常数,且对任意实数
为正的常数,且对任意实数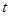 ,函数
,函数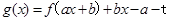 只有一个零点,当
只有一个零点,当 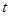 =0时,
=0时,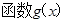 的零点
的零点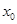 满足
满足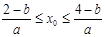 ,则点(
,则点(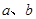 )形成的平面区域的面积为( )
)形成的平面区域的面积为( )A.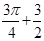 | B.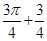 | C.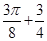 | D.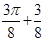 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com