
科目:高中数学 来源: 题型:
(2009天津卷文)(本小题满分12分)
为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,用列举法计算这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009天津卷文)(本小题满分12分)
为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,用列举法计算这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市海淀区高三5月期末练习(二模)文科数学试卷(解析版) 题型:选择题
已知a =
 ,b=sin
,b=sin ,c=
,c= ,则a, b,c的大小关系为
,则a, b,c的大小关系为
A.a < b < c B.a <c <b C.b <a<c D.b <c < a
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省南充市高三第二次诊断性考试理科数学卷 题型:选择题
已知A\B、C是表面积为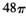 的球面上三点,且AB=2,BC=4,
的球面上三点,且AB=2,BC=4,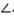 ABC=
ABC=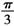 为球心,则二面角0-AB-C的大小为( )
为球心,则二面角0-AB-C的大小为( )
A.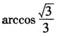 B.
B.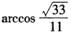 C.
C.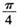 D.
D.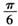
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com