Question

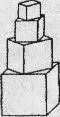
如右图，一单位正方体形积木，平放于桌面上，并且在其上方放置若干个小正方体形积木摆成塔形，其中上面正方体中下底面的四个顶点是下面相邻正方体中上底面各边的中点，如果所有正方体暴露在外面部分的面积之和超过8．8，则正方体的个数至少是

A．6    8．7    C．8    D．  10

 

Answer 1

【答案】

A

【解析】

试题分析：根据图示逐层算出露出的面积加以比较即解．解：∵要求塔形露在外面的面积超过8.8（不包括下底面），最下面的立方体棱长为1，∴最下面的立方体露出的面积为：4×（1×1）+0.5=4.5；那么上面一层假如有立方体的话露出的面积为4×0.5+0.5×0.5=2.25，这两层加起来的面积为：6.75．那么上面一层假如还有立方体的话露出的面积为4×0.25+0.25×0.25=1.0625，这三层加起来的面积为：7.8125．∴立方体的个数至少是6．故选A．

考点：表面积问题

点评：本题需注意假如上面有一层立方体的话露出的表面积为：4×正方形的面积+一半正方形的面积．