
(本小题共l2分)
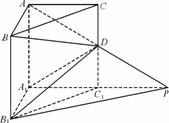 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1,延长A1C1至点P,使C1P=A1C1,连接AP交棱CC1于D.
(Ⅰ)求证:PB1∥平面BDA1;
(Ⅱ)求二面角A-A1D-B的平面角的余弦值;
本小题主要考查直三棱柱的性质、线面关系、二面角等基本知识,并考查空间想象能力和逻辑推理能力,考查应用向量知识解决问题的能力.
解法一:
(Ⅰ)连结AB1与BA1交于点O,连结OD,
∵C1D∥平面AA1,A1C1∥AP,∴AD=PD,又AO=B1O,
∴OD∥PB1,又ODÌ面BDA1,PB1Ë面BDA1,
∴PB1∥平面BDA1.
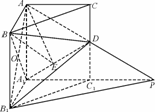 (Ⅱ)过A作AE⊥DA1于点E,连结BE.∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,
(Ⅱ)过A作AE⊥DA1于点E,连结BE.∵BA⊥CA,BA⊥AA1,且AA1∩AC=A,
∴BA⊥平面AA1C1C.由三垂线定理可知BE⊥DA1.
∴∠BEA为二面角A-A1D-B的平面角.
在Rt△A1C1D中,![]() ,
,
又![]() ,∴
,∴![]() .
.
在Rt△BAE中,![]() ,∴
,∴![]() .
.
故二面角A-A1D-B的平面角的余弦值为![]() .
.
解法二:
如图,以A1为原点,A1B1,A1C1,A1A所在直线分别为x轴,y轴,z轴建立空间直角坐标系A1-B1C1A,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
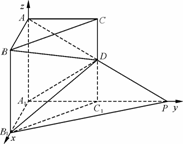 (Ⅰ)在△PAA1中有
(Ⅰ)在△PAA1中有![]() ,即
,即![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
设平面BA1D的一个法向量为![]() ,
,
则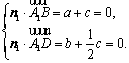 令
令![]() ,则
,则![]() .
.
∵![]() ,
,
∴PB1∥平面BA1D,
(Ⅱ)由(Ⅰ)知,平面BA1D的一个法向量![]() .
.
又![]() 为平面AA1D的一个法向量.∴
为平面AA1D的一个法向量.∴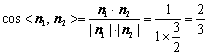 .
.
故二面角A-A1D-B的平面角的余弦值为![]() .
.


科目:高中数学 来源:2011年四川省招生统一考试理科数学 题型:解答题
(本小题共l2分)
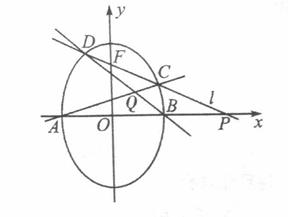
椭圆有两顶点A(-1,0)、B(1,0),过其焦点F(0,1)的直线l与椭圆交于C、D两点,并与x轴交于点P.直线AC与直线BD交于点Q.
(I)当|CD | =  时,求直线l的方程;
时,求直线l的方程;
(II)当点P异于A、B两点时,求证: 为定值.
为定值.
 [来源:ZXXK][来源:学*科*网Z*X*X*K]
[来源:ZXXK][来源:学*科*网Z*X*X*K]
查看答案和解析>>
科目:高中数学 来源:2011年四川省招生统一考试理科数学 题型:解答题
(本小题共l2分)
如图,在直三棱柱AB-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一[来源:]
P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA.
(I)求证:CD=C1D:
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离.

查看答案和解析>>
科目:高中数学 来源:2011年高考试题数学理(四川卷)解析版 题型:解答题
(本小题共l2分)
椭圆有两顶点A(-1,0)、B(1,0),过其焦点F(0,1)的直线l与椭圆交于C、D两点,并与x轴交于点P.直线AC与直线BD交于点Q.
(I)当|CD | = 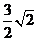 时,求直线l的方程;
时,求直线l的方程;
(II)当点P异于A、B两点时,求证: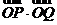 为定值。
为定值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com