
 满足:
满足: .
.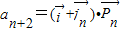 =
=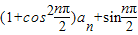 ,知a2k+1-a2k-1=1.由此能够证明数列{a2k}是首项为2、公比为2的等比数列.
,知a2k+1-a2k-1=1.由此能够证明数列{a2k}是首项为2、公比为2的等比数列.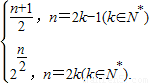 ,由此能够求出
,由此能够求出 .
.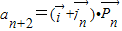 =
=
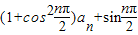 ,…(2分)
,…(2分)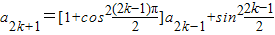 π
π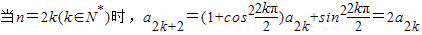 .
. …(7分)
…(7分)
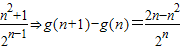 <0⇒g(n+1)<g(n)
<0⇒g(n+1)<g(n)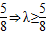 …(10分)
…(10分)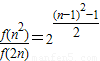
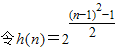 ,显然h(n)为单调递增函数,
,显然h(n)为单调递增函数, …(12分)
…(12分)

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
| OZ1 |
| OZ2 |
| OZ1 |
| OZ2 |
| 7 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年日照质检)(12分)
随着国家征收燃油税政策的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注。已知2008年1月Q型车的销量为![]() 辆,通过分析预测,若以2008年1月为第1个月,其后两年内Q型车每月的销量都将以1%的增长率增长,而R型车前n个月的销售总量Tn大致满足关系式:
辆,通过分析预测,若以2008年1月为第1个月,其后两年内Q型车每月的销量都将以1%的增长率增长,而R型车前n个月的销售总量Tn大致满足关系式:![]()
(I)求Q型车前n个月的销售总量Sn的表达式;
(2)这两款车前n个月哪款车的销售总量大?
查看答案和解析>>
科目:高中数学 来源:2012届山西大学附中高二年级五月月考数学试题(文科) 题型:解答题
已知向量 ,
, .
.
(I)若 ,求
,求 的值;
的值;
(II)在 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com