
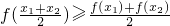 ;
;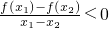 ,则函数y=f(x)是增函数.
,则函数y=f(x)是增函数.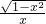 是定义在[-1,0)∪(0,1]上的奇函数
是定义在[-1,0)∪(0,1]上的奇函数 是定义在(-∞,-2]∪[2,+∞)上的奇函数
是定义在(-∞,-2]∪[2,+∞)上的奇函数 在区间(0,+∞)上也是增函数,
在区间(0,+∞)上也是增函数,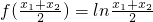 ,
,
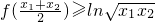
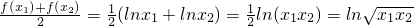
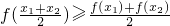 ,故③正确;
,故③正确;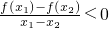 ,说明当x1<x2时,f(x1)>f(x2),
,说明当x1<x2时,f(x1)>f(x2),

科目:高中数学 来源: 题型:
A.两直线倾斜角相等,两直线平行 B.两直线斜率相等,两直线平行
C.两直线平行,两直线斜率相等 D.两直线平行,两直线倾斜角相等
查看答案和解析>>
科目:高中数学 来源:2013届云南省芒市高二上学期期末考试数学试卷 题型:选择题
下列命题正确的是 ( )
A. 两条直线确定一个平面 B. 经过三点确定一个平面
C. 经过一条直线和直线外一点确定一个平面 D. 四边形确定一个平面
查看答案和解析>>
科目:高中数学 来源:2010-2011年重庆市高二下学期检测数学试卷 题型:选择题
在空间中,下列命题正确的是
A. 两条平行直线在同一个平面之内的射影时一对平行直线
B. 平行于同一直线的两个平面平行
C. 垂直于同一平面的两个平面平行
D. 垂直于同一平面的两条直线平行
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题正确的是
①到两个定点![]() 的距离之比为常数
的距离之比为常数![]() 的动点
的动点![]() 的轨迹是圆.
的轨迹是圆.
②椭圆![]() .
.
③双曲线![]() 的焦点到渐近线的距离为
的焦点到渐近线的距离为![]() .
.
④已知点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() ,则
,则![]() .
.
A.②③④ B.①④ C.①②③ D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com