
ЗжЮі ЃЈЂёЃЉМЏКЯA3ЪєгкЕЅЕїЕндіХХСаЃЌМЏКЯB3ЪєгкЪЕЪ§ЖдЃЌРћгУСаОйЗЈБэЪОМЏКЯA3ЃЌB3МДПЩЃЛ
ЃЈЂђЃЉИљОнЬтвтжЊAn={ЃЈ1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉ}ЁЂЃЈ1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉЁЪBnЃЌЫљвдAn⊆BnЃЎЫљвдМЏКЯAnЁЩBnЕФдЊЫиИіЪ§ЮЊ1ЃЎ
ЃЈЂѓЃЉгЩЃЈЂђЃЉжЊЃЌbnЁй0ЃЎвђЮЊB2={ЃЈ1ЃЌ2ЃЉЃЌЃЈ2ЃЌ1ЃЉ}ЃЌЫљвдb2=2ЃЎЕБnЁн3ЪБЃЌПМТЧBnжаЕФдЊЫиЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉЃЎ
ЗжРрЬжТлЃКЃЈ1ЃЉМйЩшak=nЃЈ1ЁмkЃМnЃЉЃЎгЩвбжЊЃЌak+kЁмak+1+ЃЈk+1ЃЉЃЌ
вРДЫРрЭЦЃЌШєak=nЃЌдђak+1=n-1ЃЌak+2=n-2ЃЌЁЃЌan=kЃЎ
ЂйШєk=1ЃЌдђТњзуЬѕМўЕФ1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФХХСаЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉга1ИіЃЎ
ЂкШєk=2ЃЌдђa2=nЃЌa3=n-1ЃЌa4=n-2ЃЌЁЃЌan=2ЃЎ
ЂлШє2ЃМkЃМnЃЌ
ЃЈ2ЃЉМйЩшan=nЃЌжЛашЃЈa1ЃЌa2ЃЌa3ЃЌЁan-1ЃЉЪЧ1ЃЌ2ЃЌ3ЃЌЁЃЌn-1ЕФТњзуЬѕМўЕФХХСаЃЌДЫЪБТњзуЬѕМўЕФ1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФХХСаЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉгаbn-1ИіЃЎ
НсКЯЕШБШЪ§СаЕФЖЈвхНјаажЄУїЃЎ
НтД№ НтЃКЃЈЂёЃЉA3={ЃЈ1ЃЌ2ЃЌ3ЃЉ}ЃЌB3={ЃЈ1ЃЌ2ЃЌ3ЃЉЃЌЃЈ1ЃЌ3ЃЌ2ЃЉЃЌЃЈ2ЃЌ1ЃЌ3ЃЉЃЌЃЈ3ЃЌ2ЃЌ1ЃЉ}ЃЎ
ЃЈЂђЃЉПМТЧМЏКЯAnжаЕФдЊЫиЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉЃЎ
гЩвбжЊЃЌЖдШЮвтећЪ§iЃЌjЃЌ1ЁмiЃМjЁмnЃЌЖМгаai-iЁмaj-jЃЌ
ЫљвдЃЈai-iЃЉ+iЃМЃЈaj-jЃЉ+jЃЌ
ЫљвдaiЃМajЃЎ
гЩiЃЌjЕФШЮвтадПЩжЊЃЌЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉЪЧ1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФЕЅЕїЕндіХХСаЃЌ
ЫљвдAn={ЃЈ1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉ}ЃЎ
гжвђЮЊЕБak=kЃЈkЁЪN*ЃЌ1ЁмkЁмnЃЉЪБЃЌЖдШЮвтећЪ§iЃЌjЃЌ1ЁмiЃМjЁмnЃЌ
ЖМгаai+iЁмaj+jЃЎ
ЫљвдЃЈ1ЃЌ2ЃЌ3ЃЌЁЃЌnЃЉЁЪBnЃЌЫљвдAn⊆BnЃЎ
ЫљвдМЏКЯAnЁЩBnЕФдЊЫиИіЪ§ЮЊ1ЃЎ
ЃЈЂѓЃЉгЩЃЈЂђЃЉжЊЃЌbnЁй0ЃЎ
вђЮЊB2={ЃЈ1ЃЌ2ЃЉЃЌЃЈ2ЃЌ1ЃЉ}ЃЌЫљвдb2=2ЃЎ
ЕБnЁн3ЪБЃЌПМТЧBnжаЕФдЊЫиЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉЃЎ
ЃЈ1ЃЉМйЩшak=nЃЈ1ЁмkЃМnЃЉЃЎгЩвбжЊЃЌak+kЁмak+1+ЃЈk+1ЃЉЃЌ
Ыљвдak+1Ёнak+k-ЃЈk+1ЃЉ=n-1ЃЌ
гжвђЮЊak+1Ёмn-1ЃЌЫљвдak+1=n-1ЃЎ
вРДЫРрЭЦЃЌШєak=nЃЌдђak+1=n-1ЃЌak+2=n-2ЃЌЁЃЌan=kЃЎ
ЂйШєk=1ЃЌдђТњзуЬѕМўЕФ1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФХХСаЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉга1ИіЃЎ
ЂкШєk=2ЃЌдђa2=nЃЌa3=n-1ЃЌa4=n-2ЃЌЁЃЌan=2ЃЎ
Ыљвдa1=1ЃЎ
ДЫЪБТњзуЬѕМўЕФ1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФХХСаЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉга1ИіЃЎ
ЂлШє2ЃМkЃМnЃЌ
жЛвЊЃЈa1ЃЌa2ЃЌa3ЃЌЁak-1ЃЉЪЧ1ЃЌ2ЃЌ3ЃЌЁЃЌk-1ЕФТњзуЬѕМўЕФвЛИіХХСаЃЌОЭПЩвдЯргІЕУЕН1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФвЛИіТњзуЬѕМўЕФХХСаЃЎ
ДЫЪБЃЌТњзуЬѕМўЕФ1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФХХСаЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉгаbk-1ИіЃЎ
ЃЈ2ЃЉМйЩшan=nЃЌжЛашЃЈa1ЃЌa2ЃЌa3ЃЌЁan-1ЃЉЪЧ1ЃЌ2ЃЌ3ЃЌЁЃЌn-1ЕФТњзуЬѕМўЕФХХСаЃЌДЫЪБТњзуЬѕМўЕФ1ЃЌ2ЃЌ3ЃЌЁЃЌnЕФХХСаЃЈa1ЃЌa2ЃЌa3ЃЌЁЃЌanЃЉгаbn-1ИіЃЎ
злЩЯbn=1+1+b2+b3+Ё+bn-1ЃЌnЁн3ЃЎ
вђЮЊb3=1+1+b2=4=2b2ЃЌ
ЧвЕБnЁн4ЪБЃЌbn=ЃЈ1+1+b2+b3+Ё+bn-2ЃЉ+bn-1=2bn-1ЃЌ
ЫљвдЖдШЮвтnЁЪN*ЃЌnЁн3ЃЌЖМга$\frac{b_n}{{{b_{n-1}}}}=2$ЃЎ
Ыљвд{bn}ГЩЕШБШЪ§СаЃЎ
ЕуЦР БОЬтПМВщЕШБШЙиЯЕЕФШЗЖЈгыЕШВюЪ§СаЕФаджЪЃЌПМВщдЫЫугыЭЦРэЁЂжЄУїЕФФмСІЃЌФбЖШНЯДѓЃЎ


 ЬьЬьСЗПкЫуЯЕСаД№АИ
ЬьЬьСЗПкЫуЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
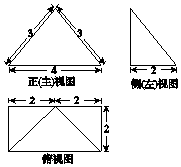
| AЃЎ | 20+2$\sqrt{5}$ | BЃЎ | 14+4$\sqrt{5}$ | CЃЎ | 26 | DЃЎ | 12+2$\sqrt{5}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
 ШчЭМЃЌдкжБШ§РтжљABC-A1B1C1жаЃЌAC=BCЃЌFЮЊA1B1ЕФжаЕуЃЎЧѓжЄЃК
ШчЭМЃЌдкжБШ§РтжљABC-A1B1C1жаЃЌAC=BCЃЌFЮЊA1B1ЕФжаЕуЃЎЧѓжЄЃКВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 26 | BЃЎ | 247 | CЃЎ | 120 | DЃЎ | 57 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com