
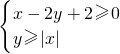 ,目标函数z=2x-y的最小值、最大值分别为a,b,则
,目标函数z=2x-y的最小值、最大值分别为a,b,则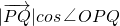 (O为原点)的取值落在区间[a,b]上的概率为________.
(O为原点)的取值落在区间[a,b]上的概率为________.
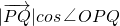 (O为原点)求出其所在的区间,最后利用几何概型的计算公式求解即得.
(O为原点)求出其所在的区间,最后利用几何概型的计算公式求解即得.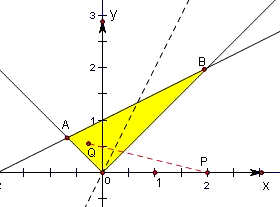 解:作出不等式组所表示的平面区域,如图所示,由z=2x-y可得y=x-z,则-z表示目标函数直线在y轴上的截距
解:作出不等式组所表示的平面区域,如图所示,由z=2x-y可得y=x-z,则-z表示目标函数直线在y轴上的截距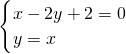 可得B(2,2),此时Z=2;
可得B(2,2),此时Z=2; 可得A(-
可得A(- ,
, ),此时Z=2
),此时Z=2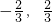 )和(2,2)取得,[a,b]=[-2,2],
)和(2,2)取得,[a,b]=[-2,2],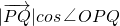 (O为原点)表示
(O为原点)表示 在x轴上射影的长度,故
在x轴上射影的长度,故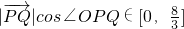 ,
, =
= .
. .
.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| MP |
| MQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| PQ |
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
| MP |
| MQ |
查看答案和解析>>
科目:高中数学 来源:2012年湖北省黄冈市英山一中高考数学模拟试卷1(理科)(解析版) 题型:解答题
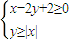 ,目标函数z=2x-y的最小值、最大值分别为a,b,则
,目标函数z=2x-y的最小值、最大值分别为a,b,则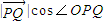 (O为原点)的取值落在区间[a,b]上的概率为 .
(O为原点)的取值落在区间[a,b]上的概率为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com