Question

在计算“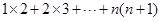”时，某同学学到了如下一种方法：先改写第k项：

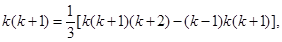由此得

  

………… 

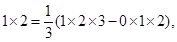
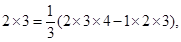
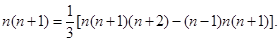
相加，得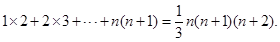

类比上述方法，请你计算“”，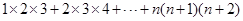

其结果为                                                   

 

Answer 1

【答案】

【解析】

试题分析：：∵n（n+1）（n+2）="1" 4 [n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]

∴1×2×3=（1×2×3×4-0×1×2×3）

2×3×4=（2×3×4×5-1×2×3×4）

…

n（n+1）（n+2）= [n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]

∴1×2×3+2×3×4+…+n（n+1）（n+2）= [（1×2×3×4-0×1×2×3）+（2×3×4×5-1×2×3×4）+…+n×（n+1）×（n+2）×（n+3）]-（n-1）×n×（n+1）×（n+2）= n(n+1)(n+2)(n+3)

故答案为： n(n+1)(n+2)(n+3)

考点：进行简单的合情推理

点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．