
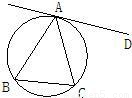
 1、如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于( )
1、如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于( ) 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
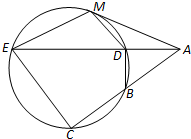 (2013•石景山区一模)如图,直线AM与圆相切于点M,ABC与ADE是圆的两条割线,且BD⊥AD,连接MD、EC.则下面结论中,错误的结论是( )
(2013•石景山区一模)如图,直线AM与圆相切于点M,ABC与ADE是圆的两条割线,且BD⊥AD,连接MD、EC.则下面结论中,错误的结论是( )查看答案和解析>>
科目:高中数学 来源: 题型:
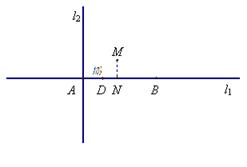
如图,直线l1与l2是同一平面内两条互相垂直的直线,交点是A,点B、D在直线l1上(B、D 位于点A右侧),且|AB|=4,|AD|=1,M是该平面上的一个动点,M在l1上的射影点是N,且|BN|=2|DM|.
(Ⅰ) 建立适当的坐标系,求动点M的轨迹C的方程.
(Ⅱ)过点D且不与l1、l2垂直的直线l交(Ⅰ)中的轨迹C于E、F两点;另外平面上的点G、H满足:①![]() ②
②![]() ③
③![]() 求点G的横坐标的取值范围.
求点G的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
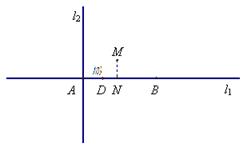
如图,直线l1与l2是同一平面内两条互相垂直的直线,交点是A,点B、D在直线l1上(B、D 位于点A右侧),且|AB|=4,|AD|=1,M是该平面上的一个动点,M在l1上的射影点是N,且|BN|=2|DM|. w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m
(Ⅰ) 建立适当的坐标系,求动点M的轨迹C的方程.
(Ⅱ)过点D且不与l1、l2垂直的直线l交(Ⅰ)中的轨迹C于E、F两点;另外平面上的点G、H满足:①![]() ②
②![]() ③
③![]() 求点G的横坐标的取值范围.
求点G的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第2章 函数):2.13 函数最值问题(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com