
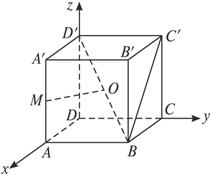
(1)证明:OM是异面直线AA′和BD′的公垂线;
(2)求异面直线MO和BC′所成的角的大小.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
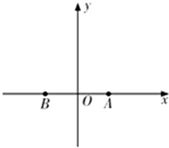 为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为10km,两镇的中心A、B相距8个单位距离,环形高速公路所在的曲线为E,且E上的点到A、B的距离之和为10个单位距离,在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离.
为了加快县域经济的发展,某县选择两乡镇作为龙头带动周边乡镇的发展,决定在这两个镇的周边修建环形高速公路,假设一个单位距离为10km,两镇的中心A、B相距8个单位距离,环形高速公路所在的曲线为E,且E上的点到A、B的距离之和为10个单位距离,在曲线E上建一个加油站M与一个收费站N,使M、N、B三点在一条直线上,并且AM+AN=12个单位距离.查看答案和解析>>
科目:高中数学 来源:2012年人教B版高中数学必修2 2.4空间直角坐标系练习卷(解析版) 题型:解答题
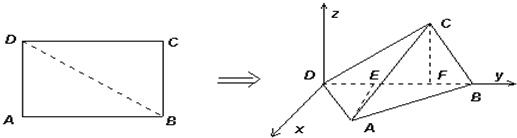
(12分)如图,已知矩形ABCD中,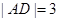 ,
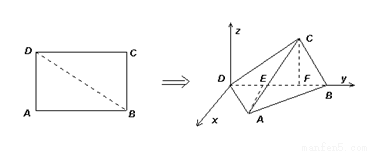
,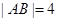 .将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com