
 的图象与x轴相切于点S(s,0).
的图象与x轴相切于点S(s,0). .
.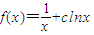 的图象与x轴相切于点S(s,0),建立方程,即可求得函数的解析式;
的图象与x轴相切于点S(s,0),建立方程,即可求得函数的解析式;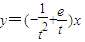 ,利用T在直线l上,可得实数t必为方程
,利用T在直线l上,可得实数t必为方程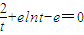 ,构造函数
,构造函数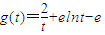 ,确定函数的单调性,从而可得
,确定函数的单调性,从而可得 是方程
是方程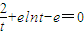 在区间
在区间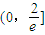 内的唯一一个解,由此可证结论;
内的唯一一个解,由此可证结论; ,利用y=tanx在
,利用y=tanx在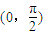 单调递增,即可证得结论.
单调递增,即可证得结论.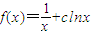 ,得
,得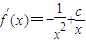 .…(1分)
.…(1分)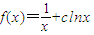 的图象与x轴相切于点S(s,0),
的图象与x轴相切于点S(s,0),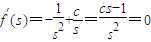 ,…①且f(s)=
,…①且f(s)=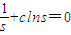 ….②…(2分)
….②…(2分)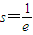 .…(3分)
.…(3分)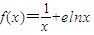 .…(4分)
.…(4分)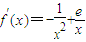 .
.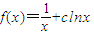 的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,
的图象与直线l相切于点T(t,f(t)),直线l过坐标原点O,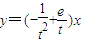 ,
,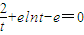 ….③的解.…(5分)
….③的解.…(5分)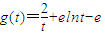 ,则
,则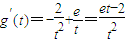 ,
, ,g′(t)<0得
,g′(t)<0得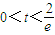 .
.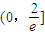 递减,在
递减,在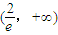 递增.…(7分)
递增.…(7分)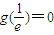 ,且函数y=g(t)在
,且函数y=g(t)在 递减,
递减,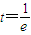 是方程
是方程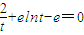 在区间
在区间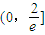 内的唯一一个解,
内的唯一一个解,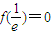 ,∴
,∴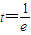 不合题意,即
不合题意,即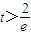 .…(8分)
.…(8分)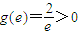 ,函数y=g(t)在
,函数y=g(t)在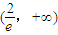 递增,
递增,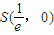
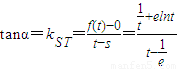 ,
,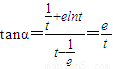 ,…(10分)
,…(10分)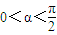 .
.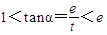 ,…(11分)
,…(11分)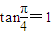 ,
,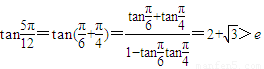 ,…(13分)
,…(13分)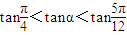 ,
,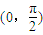 单调递增,∴
单调递增,∴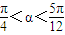 .…(14分)
.…(14分)

科目:高中数学 来源:2012-2013学年安徽省宣城市机械电子工程学校高三(上)第四次月考数学试卷(文科)(解析版) 题型:选择题
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
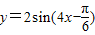
查看答案和解析>>
科目:高中数学 来源:2012年陕西省西安市西工大附中高考数学六模试卷(文科)(解析版) 题型:选择题
 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )
个单位长度得到函数y=g(x)的图象,则y=g(x)的解析式是( )

查看答案和解析>>
科目:高中数学 来源:2014届河北省高一第二学期期中理科数学试卷(解析版) 题型:解答题
.(本题12分)已知函数
 的图象与x轴交点为
的图象与x轴交点为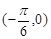 ,相邻最高点坐标为
,相邻最高点坐标为 .
.
(1)求函数 的表达式;
的表达式;
(2)求函数 的单调增区间;
的单调增区间;
(3)求函数 在
在 上的最值.
上的最值.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省高三第六次适应性训练文科数学(解析版) 题型:选择题
已知函数 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则
的图象,则 的解析式是( )
的解析式是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三第一次月考试卷理科数学 题型:选择题
已知函数 的图象与x轴的两个相邻交点的距离等于
的图象与x轴的两个相邻交点的距离等于 ,若将函数
,若将函数 的图象向左平移
的图象向左平移 个单位长度得到函数
个单位长度得到函数 的图象,则
的图象,则 的解析式是( )
的解析式是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com