
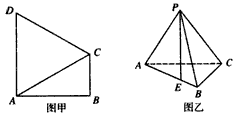
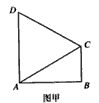
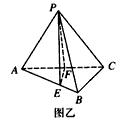
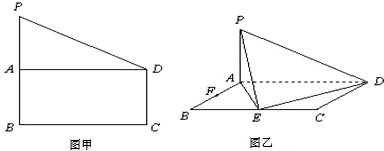
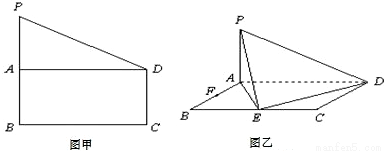
| 解法一:(Ⅰ)在图甲中, ∵ 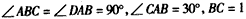 , ,∴ 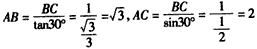 , , , ,∵AD=CD, ∴ 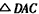 为等边三角形, 为等边三角形,∴AD=CD=AC=2, 在图乙中, ∵点E为点P在平面ABC上的正投影,∴PE⊥平面ABC, ∵BC 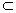 平面ABC, 平面ABC,∴PE⊥BC, ∵∠CBA= 90°, ∴BC⊥AB, ∵PE∩AB=E,PE  平面PAB,AB 平面PAB,AB 平面PAB, 平面PAB, ∴BC⊥平面PAB, ∴∠CPB为直线PC与平面PAB所成的角, 在Rt△CBP中,BC=l,PC=DC=2, ∴sin∠CPB= 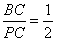 , , ∵0°<∠CPB<90°,∴∠CPB=30°, ∴直线PC与平面PAB所成的角为30°。 (Ⅱ)取AC的中点F,连接PF,EF, ∵PA=PC, ∴PF⊥AC, ∵PE⊥平面ABC,AC 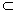 平面ABC, 平面ABC,∴PE⊥AC, ∵PF∩PE=P,PF 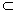 平面PEF,PE 平面PEF,PE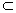 平面PEF, 平面PEF, ∴AC⊥平面PEF, ∵EF 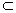 平面PEF, 平面PEF,∴EF⊥AC, ∴∠PFE为二面角P-AC-B的平面角. 在 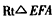 中, 中,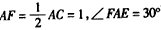 , ,∴ 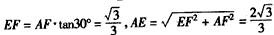 , ,在 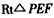 中, 中,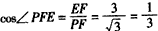 , ,∴二面角P-AC-B的大小的余弦值为 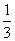 。 。 |
  |
|
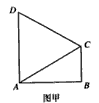
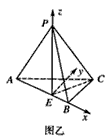
解法二:在图甲中, |
  |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市涟水县金城外国语学校高一(下)期初数学试卷(解析版) 题型:解答题
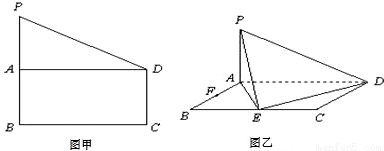
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省连云港市赣榆县海头高级中学高三数学试卷(解析版) 题型:解答题
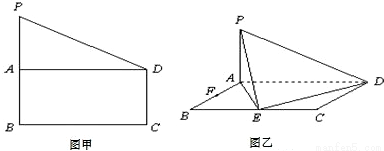
查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省常州市部分学校高三调研数学试卷(解析版) 题型:解答题
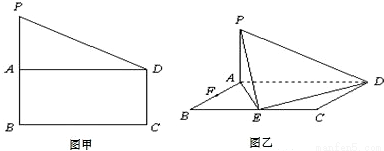
查看答案和解析>>
科目:高中数学 来源:2010年高考数学专项复习:立体几何(4)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com