
 的离心率为
的离心率为 ,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线l:x=9于G点,直线MB交直线l于H点.
,椭圆上的点到右焦点F的最近距离为2,若椭圆C与x轴交于A、B两点,M是椭圆C上异于A、B的任意一点,直线MA交直线l:x=9于G点,直线MB交直线l于H点.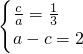 ,∴
,∴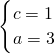 ,∴b2=a2-c2=8.
,∴b2=a2-c2=8.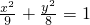 .…(4分)
.…(4分)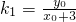 ,
,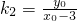 ,∴
,∴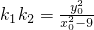 .
.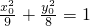 ,∴
,∴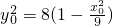 ,∴k1•k2=
,∴k1•k2= ,
,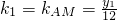 ,
,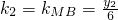 .
.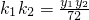 ,又k1•k2=
,又k1•k2= .∴
.∴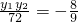 ,∴y1y2=-64.…(8分)
,∴y1y2=-64.…(8分)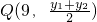 ,|GH|=|y1-y2|,
,|GH|=|y1-y2|,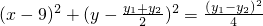 .
. 的离心率为
的离心率为 ,椭圆上的点到右焦点F的最近距离为2,建立方程组,求出几何量,从而可得椭圆C的方程;
,椭圆上的点到右焦点F的最近距离为2,建立方程组,求出几何量,从而可得椭圆C的方程; ,进一步确定以GH为直径的圆的方程,令y=0,可得定点的坐标.
,进一步确定以GH为直径的圆的方程,令y=0,可得定点的坐标.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C:| x2 |
| a2 |
| ||
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OM |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,A,B是椭圆C:
如图,A,B是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com