
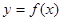 在
在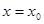 处取得极大值或极小值,则称
处取得极大值或极小值,则称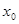 为函数
为函数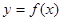 的极值点。已知
的极值点。已知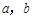 是实数,1和
是实数,1和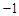 是函数
是函数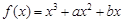 的两个极值点.
的两个极值点.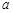 和
和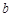 的值;
的值;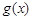 的导函数
的导函数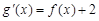 ,求
,求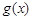 的极值点;
的极值点;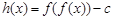 ,其中
,其中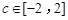 ,求函数
,求函数 的零点个数.
的零点个数.
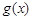 的极值点是-2
的极值点是-2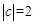 时,函数
时,函数 有5 个零点;当
有5 个零点;当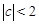 时,函数
时,函数 有9 个零点。
有9 个零点。 的导数,根据1和
的导数,根据1和 是函数
是函数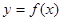 的两个极值点代入列方程组求解即可。
的两个极值点代入列方程组求解即可。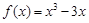 ,求出
,求出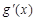 ,令
,令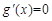 ,求解讨论即可。
,求解讨论即可。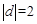 和
和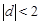 讨论关于
讨论关于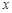 的方程
的方程 根的情况;再考虑函数
根的情况;再考虑函数 的零点
的零点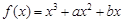 ,得
,得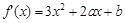 。
。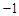 是函数
是函数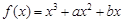 的两个极值点,
的两个极值点,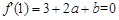 ,
,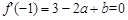 ,解得
,解得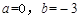 。
。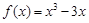 ,
,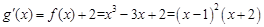 ,解得
,解得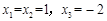 。
。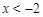 时,
时,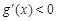 ;当
;当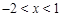 时,
时,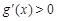 ,
,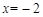 是
是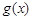 的极值点。
的极值点。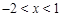 或
或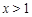 时,
时,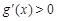 ,∴
,∴ 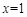 不是
不是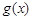 的极值点。
的极值点。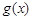 的极值点是-2。
的极值点是-2。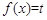 ,则
,则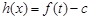 。
。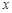 的方程
的方程 根的情况:
根的情况: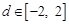
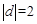 时,由(2 )可知,
时,由(2 )可知,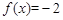 的两个不同的根为I 和一2 ,注意到
的两个不同的根为I 和一2 ,注意到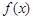 是奇函数,∴
是奇函数,∴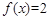 的两个不同的根为一和2。
的两个不同的根为一和2。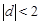 时,∵
时,∵ ,
,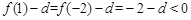 ,
, 的根。
的根。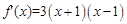 。
。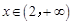 时,
时,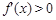 ,于是
,于是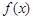 是单调增函数,从而
是单调增函数,从而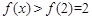 。
。 在
在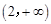 无实根。
无实根。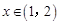 时.
时.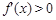 ,于是
,于是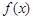 是单调增函数。
是单调增函数。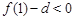 ,
,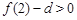 ,
,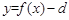 的图象不间断,
的图象不间断, 在(1 , 2 )内有唯一实根。
在(1 , 2 )内有唯一实根。 在(一2 ,一I )内有唯一实根。
在(一2 ,一I )内有唯一实根。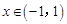 时,
时,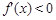 ,于是
,于是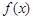 是单调减两数。
是单调减两数。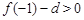 ,
, 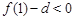 ,
,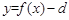 的图象不间断,
的图象不间断, 在(一1,1 )内有唯一实根。
在(一1,1 )内有唯一实根。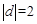 时,
时, 有两个不同的根
有两个不同的根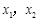 满足
满足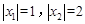 ;当
;当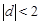 时
时 有三个不同的根
有三个不同的根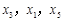 ,满足
,满足 。
。 的零点:
的零点: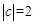 时,
时,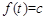 有两个根
有两个根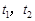 ,满足
,满足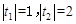 。
。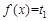 有三个不同的根,
有三个不同的根,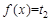 有两个不同的根,故
有两个不同的根,故 有5 个零点。
有5 个零点。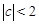 时,
时,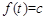 有三个不同的根
有三个不同的根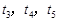 ,满足
,满足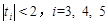 。
。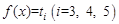 有三个不同的根,故
有三个不同的根,故 有9 个零点。
有9 个零点。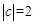 时,函数
时,函数 有5 个零点;当
有5 个零点;当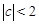 时,函数
时,函数 有9 个零点
有9 个零点

科目:高中数学 来源:不详 题型:单选题
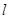 和圆
和圆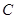 ,当
,当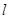 从
从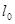 开始在平面上绕端点
开始在平面上绕端点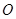 按逆时针方向匀速转动(转动角度不超过
按逆时针方向匀速转动(转动角度不超过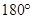 )时,它扫过的圆内阴影部分的面积
)时,它扫过的圆内阴影部分的面积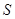 是时间
是时间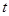 的函数,这个函数的图象大致是( ▲ )
的函数,这个函数的图象大致是( ▲ )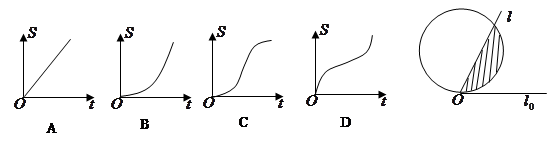
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 的图象如上右图所示。
的图象如上右图所示。
| x | -1 | 0 | 2 | 3 | 4 |
| f(x) | 1 | 2 | 0 | 2 | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com