
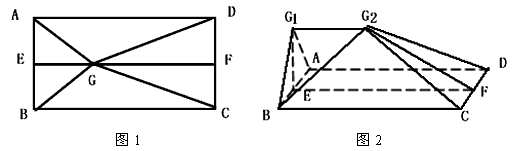
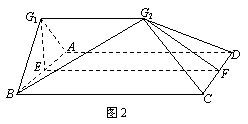
| (Ⅰ)证明:因为平面G1AB⊥平面ABCD, 平面G1AB∩平面ABCD=AB, AD⊥AB,AD  平面ABCD, 平面ABCD,所以AD⊥平面G1AB, 又AD  平面G1ADG2, 平面G1ADG2,所以平面G1AB⊥平面G1ADG2。 |
|
| (Ⅱ)解:过点B作BH⊥AG1于点H,连结G2H, 由(Ⅰ)的结论可知,BH⊥平面G1ADG2, 所以∠BG1H是BG2和平面G1ADG2所成的角, 因为平面G1AB⊥平面ABCD,平面G1AB∩平面ABCD=AB, G1E=AB,G1E  平面G1AB, 平面G1AB,所以G1E⊥平面ABCD, 故G1E⊥EF, 因为G1G2<AD,AD=EF, 所以可在EF上取一点O,使EO=G1G2, 又因为G1G2∥AD∥EO, 所以四边形G1EOG2是矩形, 由题设AB=12,BC=25,EG=8,则GF=17, 所以G2O=G1E=8,G2F=17, OF=  , ,因为AD⊥平面G1AB,G1G2∥AD, 所以G1G2⊥平面G1AB, 从而G1G2⊥G1B, 故BG  =BE2+EG =BE2+EG +G1G +G1G =62+82+102=200, =62+82+102=200,BG2=  , ,又AG1=  , ,由  , ,故  , ,即直线BG2与平面G1ADG2所成的角是  。 。 |
 |


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
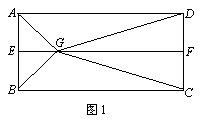
 如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.
如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
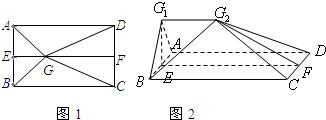
 如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.
如图1,E,F分别是矩形ABCD的边AB,CD的中点,G是EF上的一点,将△GAB,△GCD分别沿AB,CD翻折成△G1AB,△G2CD,并连接G1G2,使得平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD、连接BG2,如图2.查看答案和解析>>
科目:高中数学 来源:2007年湖南省高考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:重庆市西南师大附中09-10学年高二下学期期中考试(理) 题型:解答题
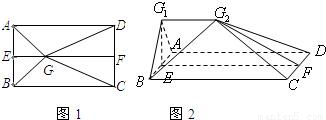
如图1,E、F分别是矩形ABCD的边AB、CD的中点,G是EF上的一点,将△GAB、△GCD分别沿AB、CD翻折成△G1AB、△G2CD,并连接G1G2,使平面G1AB⊥平面ABCD,G1G2∥AD,且G1G2<AD,连结BG2如图2.
(1) 证明平面G1AB⊥平面G1ADG2;
(2) 当AB = 12,BC = 25,EG = 8时,求直线BG2与平面G1ADG2成角.
 |
 |
||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com