

图1-3-16
(1)在这个四棱锥中放入一个球求球的最大半径;
(2)求四棱锥外接球的半径.
思路分析:(1)当所放的球与四棱锥各面都相切时球的半径最大,即球心到各个面的距离均相等,联想到用体积法求解.(2)四棱锥的外接球的球心到P、A、B、C、D五点的距离均为半径,只要找出球心的位置即可.在Rt△PDB中,斜边PB的中点为F,则PF=FB=FD,只要证明FA=FC=FP即可.
解:(1)设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连结SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,设它们的高均为R.
VP—ABCD=![]() ·S
·S![]() ABCD·PD=
ABCD·PD=![]() ·a·a·a=
·a·a·a=![]() a3,
a3,
S△PAD=S△PDC=![]() ·a·a=
·a·a=![]() a2,
a2,
S△PAB=S△PBC=![]() ·a·
·a·![]() a=
a=![]() a2,
a2,
S![]() ABCD=a2.
ABCD=a2.
VP—ABCD=VS—PDA+VS—PDC+VS—ABCD+VS—PAB+VS—PBC,
![]() a3=
a3=![]() R(S△PAD+S△PDC+S△PAB+S△PBC+S
R(S△PAD+S△PDC+S△PAB+S△PBC+S![]() ABCD),
ABCD),
![]() a3=
a3=![]() R(
R(![]() a2+
a2+![]() a2+
a2+![]() a2+
a2+![]() a2+a2),
a2+a2),
所以![]() (2+
(2+![]() )a2=
)a2=![]() a3,
a3,
R=![]() a=(1-
a=(1-![]() )a,
)a,
即球的最大半径为(1-![]() )a.
)a.
(2)设PB的中点为F.
因为在Rt△PDB中,FP=FB=FD,
在Rt△PAB中,FA=FP=FB,
在Rt△PBC中,FP=FB=FC,
所以FP=FB=FA=FC=FD.
所以F为四棱锥外接球的球心,
则FP为外接球的半径.
因为FB=![]() PB,所以FB=
PB,所以FB=![]() a,
a,
所以四棱锥外接球的半径为![]() a.
a.


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |
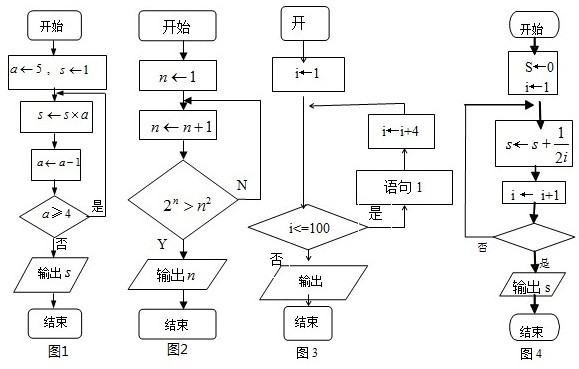
查看答案和解析>>
科目:高中数学 来源: 题型:

图1-3-9
A.11.25 m B.6.6 m C.8 m D.10.5 m
查看答案和解析>>
科目:高中数学 来源: 题型:
分数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数 | 1 | 3 | 5 | 7 | 6 | 8 | 6 | 4 | 3 | 2 |
B班的成绩如图2-2-16所示.
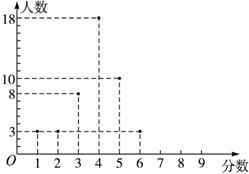
图2-2-16
(1)你认为哪个班级的成绩比较稳定?
(2)若两班共有60人及格,则参加者最少获得多少分才可能及格?
查看答案和解析>>
科目:高中数学 来源: 题型:

图1-3-11
A.11.25 m B.6.6 m C.8 m D.10.5 m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com