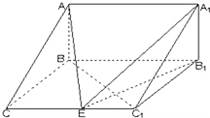
如图,在三棱拄ABC﹣A
1B
1C
1中,AB⊥侧面BB
1C
1C,已知
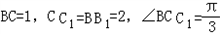
(Ⅰ)求证:C
1B⊥平面ABC;
(Ⅱ)试在棱CC
1(不包含端点C,C
1)上确定一点E的位置,使得EA⊥EB
1;
(Ⅲ) 在(Ⅱ)的条件下,求二面角A﹣EB
1﹣A
1的平面角的正切值.
证明:(Ⅰ)因为AB⊥侧面BB
1C
1C,故AB⊥BC
1
在△BC
1C中,
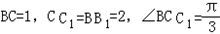
由余弦定理有
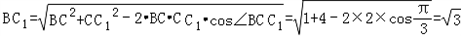
故有BC
2+BC
12=CC
12
∴C
1B⊥BC
而BC∩AB=B且AB,BC
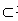
平面ABC
∴C
1B⊥平面ABC
(Ⅱ)由EA⊥EB
1,AB⊥EB
1,AB∩AE=A,AB,AE
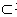
平面ABE
从而B
1E⊥平面ABE且BE
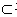
平面ABE故BE⊥B
1E
不妨设CE=x,则C
1E=2﹣x,则BE
2=1+x
2﹣x
又∵
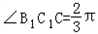
则B
1E
2=1+x
2+x
在Rt△BEB
1中有x
2+x+1+x
2﹣x+1=4从而x=±1(舍负)
故E为CC
1的中点时,EA⊥EB
1
(Ⅲ)取EB
1的中点D,A
1E的中点F,BB
1的中点N,AB
1的中点M
连DF则DF∥A
1B
1,连DN则DN∥BE,连MN则MN∥A
1B
1
连MF则MF∥BE,且MNDF为矩形,MD∥AE
又∵A
1B
1⊥EB
1,BE⊥EB
1故∠MDF为所求二面角的平面角
在Rt△DFM中,
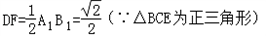
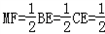
∴
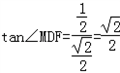
练习册系列答案
相关习题
科目:高中数学
来源:
题型:
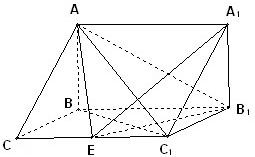
如图,在三棱拄ABC-A
1B
1C
1中,AB⊥侧面BB
1C
1C,已知BC=1,BB
1=C
1C,∠BCC
1=
,
(1)求证:C
1B⊥平面ABC;
(2)试在棱CC
1(不包含端点C,C
1上确定一点E的位置,使得EA⊥EB
1;
(3)在(2)的条件下,求二面角A-EB
1-A
1的平面角的正切值.
查看答案和解析>>
科目:高中数学
来源:
题型:
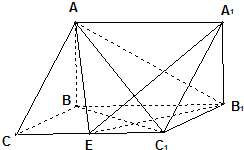
如图,在三棱拄ABC-A
1B
1C
1中,AB⊥侧面BB
1C
1C,已知
BC=1,CC1=BB1=2,∠BCC1=(Ⅰ)求证:C
1B⊥平面ABC;
(Ⅱ)试在棱CC
1(不包含端点C,C
1)上确定一点E的位置,使得EA⊥EB
1;
(Ⅲ)在(Ⅱ)的条件下,AB=
,求二面角A-EB
1-A
1的平面角的正切值.
查看答案和解析>>
科目:高中数学
来源:黑龙江省模拟题
题型:解答题
如图,在三棱拄ABC-A
1B
1C
1中,AB⊥侧面BB
1C
1C,已知BC=1,CC
1=2,AB=

, ∠BCC
1=

。
(1)求证:C
1B⊥平面ABC;
(2)当E为CC
1的中点时,求二面角A-EB
1-A
1的平面角的正切值。
查看答案和解析>>
科目:高中数学
来源:2011-2012学年江西省景德镇乐平中学高三(上)10月月考数学试卷(理科)(解析版)
题型:解答题

如图,在三棱拄ABC-A
1B
1C
1中,AB⊥侧面BB
1C
1C,已知

(Ⅰ)求证:C
1B⊥平面ABC;
(Ⅱ)试在棱CC
1(不包含端点C,C
1)上确定一点E的位置,使得EA⊥EB
1;
(Ⅲ)在(Ⅱ)的条件下,AB=

,求二面角A-EB
1-A
1的平面角的正切值.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年广东省清远市英德一中高三(上)期末数学复习试卷1(理科)(解析版)
题型:解答题
如图,在三棱拄ABC-A
1B
1C
1中,AB⊥侧面BB
1C
1C,已知BC=1,BB
1=C
1C,∠BCC
1=
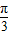
,
(1)求证:C
1B⊥平面ABC;
(2)试在棱CC
1(不包含端点C,C
1上确定一点E的位置,使得EA⊥EB
1;
(3)在(2)的条件下,求二面角A-EB
1-A
1的平面角的正切值.

查看答案和解析>>

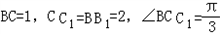
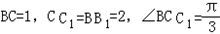
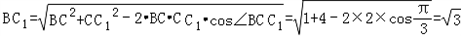
 平面ABC
平面ABC
 平面ABE
平面ABE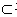 平面ABE故BE⊥B1E
平面ABE故BE⊥B1E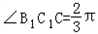 则B1E2=1+x2+x
则B1E2=1+x2+x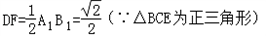
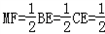
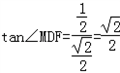
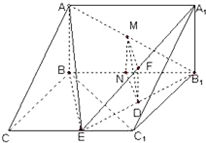


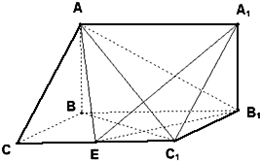
 如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=C1C,∠BCC1=
如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,BB1=C1C,∠BCC1= 如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1=
如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BC=1,CC1=BB1=2,∠BCC1= , ∠BCC1=
, ∠BCC1=  。
。
 如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知
如图,在三棱拄ABC-A1B1C1中,AB⊥侧面BB1C1C,已知
 ,求二面角A-EB1-A1的平面角的正切值.
,求二面角A-EB1-A1的平面角的正切值.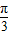 ,
,