
已知数列 的前
的前 项和为
项和为 ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)求证:数列 是等比数列.
是等比数列.
(1) ,
, ;(2)证明见解析
;(2)证明见解析
解析试题分析:(1)给出 与
与 的关系,求
的关系,求 ,常用思路:一是利用
,常用思路:一是利用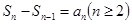 转化为
转化为 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为 的递推关系,先求出
的递推关系,先求出 与
与 的关系,再求
的关系,再求 ;(2)数列的递推关系是给出数列的一种方法,根据给出的初始值和递推关系可以依次写出这个数列的各项,再由递推关系求数列的通项公式,常用方法有:一是求出数列的前几项,再归纳总结出数列的一个通项公式;二是将已知递推关系式整理、变形,变成等差数列或者等比数列,或用累加法,累乘法,迭代法求通项.
;(2)数列的递推关系是给出数列的一种方法,根据给出的初始值和递推关系可以依次写出这个数列的各项,再由递推关系求数列的通项公式,常用方法有:一是求出数列的前几项,再归纳总结出数列的一个通项公式;二是将已知递推关系式整理、变形,变成等差数列或者等比数列,或用累加法,累乘法,迭代法求通项.
试题解析:(1)当 时,
时,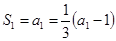 ,解得
,解得 ,当
,当 时,
时, ,解得
,解得
由于 当
当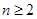 时,
时, ,两式相减得
,两式相减得 ,整理得
,整理得 ,所以数列
,所以数列 为等比数列.
为等比数列.
考点:(1)求数列各项的值;(2)证明数列为等比数列.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com