
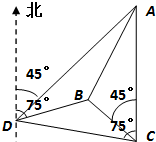
 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进| 6 |
| DCsin∠BDC |
| sin∠DBC |
| 2 |
| 6 |
| DCsin∠ADC |
| sin∠DAC |
| ||
| sin45° |
| 6 |
| DCsin∠BDC |
| sin∠DBC |
| ||
| sin120° |
| 2 |
| 2 |
| 5 |
| 5 |


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进| 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
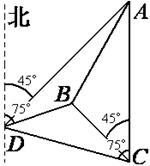
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进![]() km到达D,看到A在他的北偏东45°方向,B在其的北偏东75°方向,试求这两座建筑物之间的距离.
km到达D,看到A在他的北偏东45°方向,B在其的北偏东75°方向,试求这两座建筑物之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
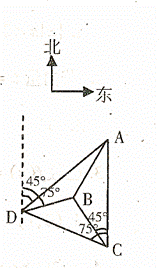
如图,一人在C地看到建筑物A正北方向,另一建筑物B在北偏西![]() 方向,此人向北偏西
方向,此人向北偏西![]() 方向前进
方向前进![]() 到达D处,看到A在他的北偏东
到达D处,看到A在他的北偏东![]() 方向,B在北偏东
方向,B在北偏东![]() 方向,试求这两座建筑物之间的距离.
方向,试求这两座建筑物之间的距离.
查看答案和解析>>
科目:高中数学 来源:2011年陕西省咸阳市高考数学模拟考试试卷2(理科)(解析版) 题型:解答题
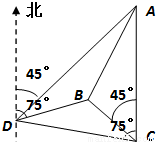 如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进
如图,一人在C地看到建筑物A在正北方向,另一建筑物B在北偏西45°方向,此人向北偏西75°方向前进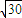 km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.
km到达D处,看到A在他的北偏东45°方向,B在北偏东75°方向,试求这两座建筑物之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com