
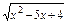 ;
;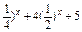 .
. 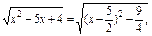 ∵x∈(-∞,1]∪[4,+∞),
∵x∈(-∞,1]∪[4,+∞),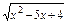 ≥0,而f(x)=3
≥0,而f(x)=3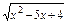 ≥30=1,
≥30=1,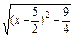 ,∴当x∈(-∞,1]时,u是减函数,
,∴当x∈(-∞,1]时,u是减函数,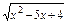 在(-∞,1]上是减函数,在[4,+∞)上是增函数.
在(-∞,1]上是减函数,在[4,+∞)上是增函数.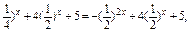
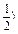 x (t>0),∴g(t)=-t2+4t+5=-(t-2)2+9,
x (t>0),∴g(t)=-t2+4t+5=-(t-2)2+9,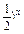 =2,即x=-1,∴g(x)的值域是(-∞,9].
=2,即x=-1,∴g(x)的值域是(-∞,9].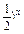 是减函数,∴要求g(x)的增区间实际上是求g(t)的减区间,
是减函数,∴要求g(x)的增区间实际上是求g(t)的减区间,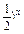 ≤2,可得x≥-1,由t=(
≤2,可得x≥-1,由t=(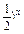 ≥2,可得x≤-1.
≥2,可得x≤-1.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源:不详 题型:解答题
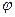 (x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,
(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,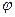 (
(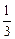 )=16,
)=16,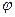 (1)=8.
(1)=8.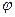 (x)的解析式,并指出定义域;
(x)的解析式,并指出定义域;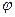 (x)的值域.
(x)的值域.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com