
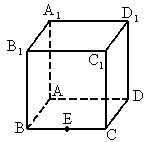
如图所示,在棱长为1的正方体ABCD- 中,点E是棱BC的中点,点F是棱CD上的动点.
中,点E是棱BC的中点,点F是棱CD上的动点.
(1)试确定点F的位置,使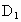 E⊥平面A
E⊥平面A F;
F;
(2)当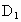 E⊥平面A
E⊥平面A F时,求二面角
F时,求二面角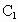 -EF-A的大小(结果用反三角函数值表示).
-EF-A的大小(结果用反三角函数值表示).
|
本小题主要考查线面关系和正方体等基础知识,考查空间想象能力和推理运算能力. 解: (1)连结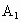 B,∵ B,∵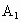  ∥BC, ∥BC,
∴ 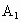 ,B,E, ,B,E, 四点共面,如图所示. 四点共面,如图所示.
在正方形 AB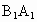 中, 中,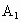 B⊥A B⊥A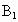 , ,
∵ BE⊥平面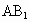 ,A ,A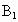  平面A 平面A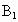 , ,
∴ 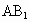 ⊥BE.∵ ⊥BE.∵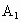 B∩BE=B, B∩BE=B,
∴ 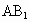 ⊥平面 ⊥平面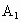 BE BE . .
又  E E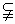 平面 平面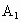 BE BE ,∴ ,∴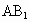 ⊥ ⊥ E. E.
若要使  E⊥平面A E⊥平面A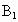 F,则必有 F,则必有 E⊥AF. E⊥AF.
连结 DE,由于 D⊥平面AC,AF D⊥平面AC,AF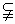 平面AC, 平面AC,
∴  D⊥AF.要有AF⊥ D⊥AF.要有AF⊥ E,∴应有AF⊥DE. E,∴应有AF⊥DE.
如图所示,由于 E是BC的中点,若要 AF⊥DE,则∠DGF=90°,∵∠ FDG+∠DEC=90°,又必有∠ FDG+∠DFG=90°,从而应有∠ DFG=∠DEC,∴△ ADF≌△DCE,∴F应为DC的中点.∴当 F为DC的中点时, E⊥平面A E⊥平面A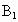 F. F.
(2) 略.把握几何图形特征求解. |


科目:高中数学 来源:2015届海南琼海嘉积中学高一下学期教学监测(二)理数学卷(解析版) 题型:选择题
如图所示,在棱长为1的正方体 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 最短,则
最短,则 的最小值为( )
的最小值为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省温州市八校高一下学期期末联考试卷数学 题型:选择题
如图所示,在棱长为1的正方体 的面
的面
对角线 上存在一点
上存在一点 使得
使得 取得最小值,则此
取得最小值,则此
最小值为 ( )
A.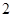 B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com