曲线y=2lnx上的点到直线x-y+1=0的最短距离是 .
【答案】
分析:设直线x-y+C=0是曲线y=2lnx的切线且与直线x-y+1=0平行,利用导数的几何意义求出切点坐标为P(2,2ln2)
,再由点到直线的距离公式,即可算出曲线y=2lnx上的点到直线x-y+1=0的最短距离.
解答:解:设直线x-y+C=0与直线x-y+1=0平行,
且与曲线y=2lnx相切,切点为P(m,2lnm)
∴y'
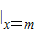
=1,即
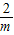
=1,可得m=2,切点为P(2,2ln2)
求得P到直线x-y+1=0的距离d=
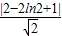
=
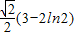
即曲线y=2lnx上的点到直线x-y+1=0的最短距离是
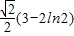
故答案为:
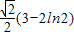 点评:
点评:本题求曲线上动点到直线的最短距离,着重考查了点到直线的距离公式和导数的几何意义等知识,属于基础题.

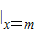 =1,即
=1,即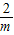 =1,可得m=2,切点为P(2,2ln2)
=1,可得m=2,切点为P(2,2ln2)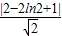 =
=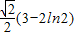
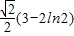
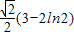


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案