
设P是⊙O: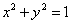 上的一点,以
上的一点,以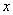 轴的非负半轴为始边、OP为终边的角记为
轴的非负半轴为始边、OP为终边的角记为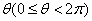 ,又向量
,又向量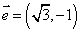 。且
。且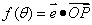 .
.
(1)求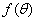 的单调减区间;
的单调减区间;
(2)若关于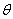 的方程
的方程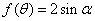 在
在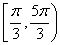 内有两个不同的解,求
内有两个不同的解,求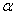 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
现有两个命题:
(1)若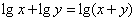 ,且不等式
,且不等式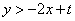 恒成立,则
恒成立,则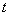 的取值范围是集合
的取值范围是集合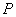 ;
;
(2)若函数 ,
,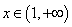 的图像与函数
的图像与函数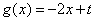 的图像没有交点,则
的图像没有交点,则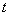 的取值范围是集合
的取值范围是集合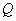 ;
;
则以下集合关系正确的是( )
A.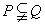 B.
B.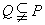 C.
C.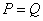 D.
D.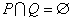
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[l04,l06].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是( )

A.90 B.75 C.60 D.45
查看答案和解析>>
科目:高中数学 来源: 题型:
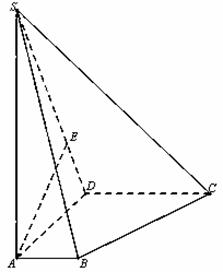
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA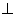 底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且
底面ABCD,且SA=2,AD=DC=1, 点E在SD上,且 .
.
(1)证明: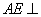 平面
平面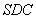 ;
;
(2)求三棱锥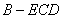 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
一支田径队有男女运动员98人,其中男运动员有56人.按男女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com