
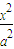 +
+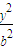 =1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数y=asinx+3bcosx图象的一条对称轴的方程是
=1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数y=asinx+3bcosx图象的一条对称轴的方程是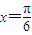 .(1)求椭圆C的离心率e与直线AB的方程;(2)对于任意一点M∈C,试证:总存在角θ(θ∈R)使等式
.(1)求椭圆C的离心率e与直线AB的方程;(2)对于任意一点M∈C,试证:总存在角θ(θ∈R)使等式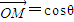
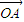 +sinθ
+sinθ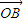 成立.
成立.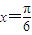 .推出f(
.推出f(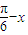 )=f(
)=f(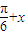 ),利用取
),利用取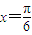 ,整理得a=
,整理得a= b,求出离心率,求出焦点坐标然后求出直线方程;
b,求出离心率,求出焦点坐标然后求出直线方程; 与
与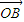 是平面内的两个不共线的向量,由平面向量的基本定理,表示
是平面内的两个不共线的向量,由平面向量的基本定理,表示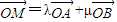 ,设M(x,y),通过坐标运算,推出x=λx1+μx2,y=λy1+μy2.代入椭圆方程,推出x1x2+3y1y2=0,由A,B两点在椭圆上,整理出λ2+μ2=1.根据圆的参数方程可知,总存在角θ,θ∈R使等式
,设M(x,y),通过坐标运算,推出x=λx1+μx2,y=λy1+μy2.代入椭圆方程,推出x1x2+3y1y2=0,由A,B两点在椭圆上,整理出λ2+μ2=1.根据圆的参数方程可知,总存在角θ,θ∈R使等式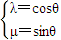 成立,就是
成立,就是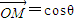
 +sinθ
+sinθ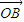 成立.
成立.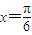 .所以对任意的实数x都有f(
.所以对任意的实数x都有f( )=f(
)=f(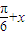 ),
),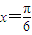 得f(0)=f(
得f(0)=f( ),整理得a=
),整理得a=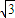 b,
b,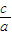 =
=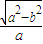 =
=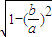 =
=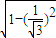 =
=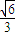 .
.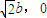 )
)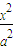 +
+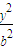 =1(a>b>0)右焦点F且斜率为1的直线,
=1(a>b>0)右焦点F且斜率为1的直线,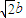 .
.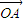 与
与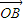 是平面内的两个不共线的向量,由平面向量的基本定理,对于这一平面内的向量
是平面内的两个不共线的向量,由平面向量的基本定理,对于这一平面内的向量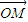 ,有且只有一对实数λ,μ.使得
,有且只有一对实数λ,μ.使得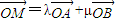 成立.
成立.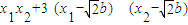
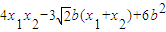 =3b2-9b2+6b2=0.
=3b2-9b2+6b2=0.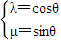 成立.
成立.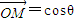
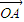 +sinθ
+sinθ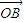 成立.
成立.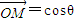
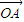 +sinθ
+sinθ 成立.
成立.

科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| OM |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| OM |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省天门市高三模拟考试(二)理科数学 题型:解答题
(本小题满分13分)
已知过椭圆C: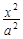 +
+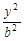 =1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数
=1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数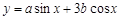 图象的一条对称轴的方程是
图象的一条对称轴的方程是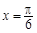 .
.
(1)求椭圆C的离心率e与直线AB的方程;
(2)对于任意一点M∈C,试证:总存在角θ(θ∈R)使等式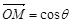
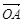 +
+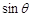
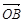 成立.
成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com