
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1 , AA1=AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的点,AB1 , DF交于点E,且AB1⊥DF,则下列结论中不正确的是( ) 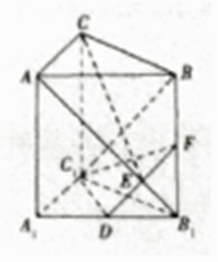
A.CE与BC1异面且垂直
B.AB1⊥C1F
C.△C1DF是直角三角形
D.DF的长为 ![]()
【答案】D
【解析】解:对于A,∵BC1平面B1C1CB,CE平面B1C1CB,且C∈平面B1C1CB,
∴CE与BC1是异面直线,
∵AA1∥CC1,AA1⊥平面ABC,
∴CC1⊥平面ABC,∴CC1⊥AC,
又AC⊥BC,BC∩CC1=C,
∴AC⊥平面B1C1CB,又BC1平面B1C1CB,
∴AC⊥BC1,
又四边形B1C1CB是正方形,∴BC1⊥B1C,
又B1C∩AC=C,
∴BC1⊥平面AB1C,∵CE平面AB1C,
∴BC1⊥CE,故A正确;
对于B,∵C1A1=C1B1,D是A1B1的中点,∴C1D⊥A1B1,
由AA1⊥底面A1B1C1可得AA1⊥C1D,
又A1B1∩AA1=A1,∴C1D⊥平面ABB1A1,
∴C1D⊥AB1,又DF⊥AB1,C1D∩DF=D,
∴AB1⊥平面C1DF,
∴AB1⊥C1F,故B正确;
对于C,由C1D⊥平面ABB1A1可得C1D⊥DF,
故△C1DF是直角三角形,故C正确;
对于D,∵AC=BC=AA1=1,∠ACB=90°,
∴A1B1=AB= ![]() ,AB1=
,AB1= ![]() ,∴DB1=
,∴DB1= ![]() ,
,
∵AB1⊥DF,∴∠FDB1=∠AB1F=∠A1AB1,
∴cos∠FDB1=cos∠A1AB1,即 ![]() ,
,
∴ ![]() ,解得DF=
,解得DF= ![]() ,故D错误.
,故D错误.
故选D.
【考点精析】根据题目的已知条件,利用空间中直线与直线之间的位置关系的相关知识可以得到问题的答案,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |

(1)作出这些数据的频数分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中间值来代表这种产品质量的指标值);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的85%”的规定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣ax,g(x)= ![]() x2﹣lnx﹣
x2﹣lnx﹣ ![]() .
.
(1)若f(x)和g(x)在同一点处有相同的极值,求实数a的值;
(2)对于一切x∈(0,+∞),有不等式f(x)≥2xg(x)﹣x2+5x﹣3恒成立,求实数a的取值范围;
(3)设G(x)= ![]() x2﹣
x2﹣ ![]() ﹣g(x),求证:G(x)>
﹣g(x),求证:G(x)> ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是偶函数,f(x+1)是奇函数,且对任意的x1 , x2∈[0,1],且x1≠x2 , 都有(x1﹣x2)[f(x1)﹣f(x2)]<0,设a=f( ![]() ),b=﹣f(
),b=﹣f( ![]() ),c=f(
),c=f( ![]() ),则下列结论正确的是( )
),则下列结论正确的是( )
A.a>b>c
B.b>a>c
C.b>c>a
D.c>a>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点C到点F(1,0)的距离比到直线x=﹣2的距离小1,动点C的轨迹为E.
(1)求曲线E的方程;
(2)若直线l:y=kx+m(km<0)与曲线E相交于A,B两个不同点,且 ![]() ,证明:直线l经过一个定点.
,证明:直线l经过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C的对边分别为a,b,c,且tanA,tanB是关于x的方程x2+(1+p)x+p+2=0的两个根,c=4.
(1)求角C的大小;
(2)求△ABC面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣3)2=2被y轴截得的线段AB与被直线y=3x+b所截得的线段CD的长度相等,则b等于( )
A.± ![]()
B.± ![]()
C.±2 ![]()
D.± ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个总体中有600个个体,随机编号为001,002,…,600,利用系统抽样方法抽取容量为24的一个样本,总体分组后在第一组随机抽得的编号为006,则在编号为051~125之间抽得的编号为( )
A.056,080,104
B.054,078,102
C.054,079,104
D.056,081,106
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x=﹣3,x=1是函数f(x)=sin(ωx+φ)(ω>0)的两个相邻的极值点,且f(x)在x=﹣1处的导数f'(﹣1)>0,则f(0)=( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com