Question

不等式組 l

x≥0 y≥0 x+y- 2 -1≤0 x-ky+k≥0

表示的是一个轴对称四边形围成的区域，则k=

 

．

Answer 1

分析：我们先画出约束条件中不含参数的几个不等式表示的平面区域，根据该平面区域的形状是一个轴对称四边形围成的区域，和含参数的直线所表示的意义，分析满足条件的k的取值．

解答：解：不等式组l

x≥0 y≥0 x+y- 2 -1≤0 x-ky+k≥0

将前三个不等式所表示的平面区域，
三个顶点分别为（0，0），（

2

+1，0），（0，

2

+1），
第四个不等式x-ky+k≥0，表示的是横过点（0，1）的直线，

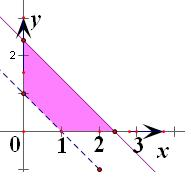
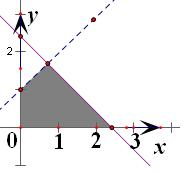
如图，当k=-1或1时不等式组所表示是一个轴对称四边形围成的区域，
故答案为：±1

点评：平面区域的形状问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合分类讨论的思想，针对图象分析满足条件的参数的取值范围．