
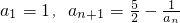 ,
,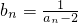 ,则数列{bn}的通项公式bn=________.
,则数列{bn}的通项公式bn=________.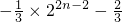
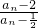 是等比数列,求出通项公式,然后求出an的通项公式,最后求解数列{bn}的通项公式bn.
是等比数列,求出通项公式,然后求出an的通项公式,最后求解数列{bn}的通项公式bn.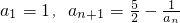
 )an=5an-2-an=4(an-
)an=5an-2-an=4(an- )
)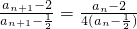
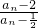 ,c1=
,c1= =-2,cn+1=
=-2,cn+1= cn,
cn,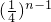 =-2•2-2n+2=-2-2n+3.
=-2•2-2n+2=-2-2n+3.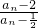 =-2-2n+3.
=-2-2n+3. )•2-2n+3=-an2-2n+3+2-2n+2
)•2-2n+3=-an2-2n+3+2-2n+2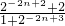 ,
,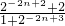 -2
-2
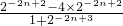
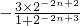
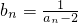 =-
=- ×
×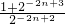
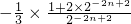
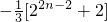
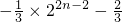 .
.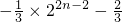 .
.

科目:高中数学 来源: 题型:
| Sn |
| n |
| b1+b2+…+bn |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
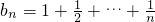 ,试判断数列{bn}是否有上界.
,试判断数列{bn}是否有上界.查看答案和解析>>
科目:高中数学 来源:2012年上海市黄浦区、嘉定区高考数学二模试卷(理科)(解析版) 题型:解答题
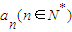 表示A型车床在第n年创造的价值.
表示A型车床在第n年创造的价值.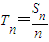 .企业经过成本核算,若Tn>100万元,则继续使用A型车床,否则更换A型车床.试问该企业须在第几年年初更换A型车床?(已知:若正数数列{bn}是单调递减数列,则数列
.企业经过成本核算,若Tn>100万元,则继续使用A型车床,否则更换A型车床.试问该企业须在第几年年初更换A型车床?(已知:若正数数列{bn}是单调递减数列,则数列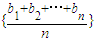 也是单调递减数列).
也是单调递减数列).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com