
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:高中数学 来源:辽宁省沈阳四校协作体2012届高三12月月考数学理科试题 题型:044
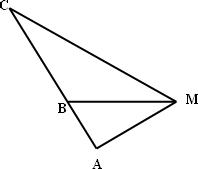
如图已知A,B,C是一条直路上的三点,AB=1 km,BC=2 km,从三点分别遥望塔M,在A处看见塔在北偏东60°,在B处看见塔在正东方向,在C处看见塔在南偏东60°,求塔M到直路ABC的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
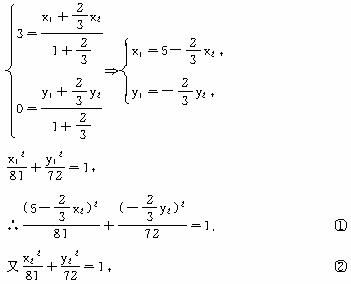
(1)求点P的轨迹方程;
(2)经过点C的直线l与点P的轨迹交于M、N两点,且点C分![]() 所成的比等于2∶3,求直线l的方程.
所成的比等于2∶3,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
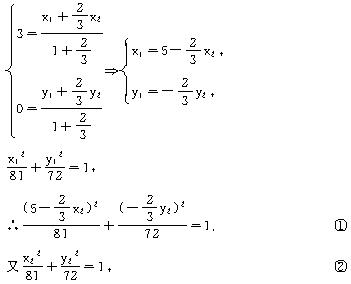
(1)求点P的轨迹方程;
(2)经过点C的直线l与点P的轨迹交于M、N两点,且点C分![]() 所成的比等于2∶3,求直线l的方程.
所成的比等于2∶3,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:四边形EFHG是一个平行四边形;
(2)若AB=CD=a,试求四边形EFGH的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com