
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】
(1)解:设等差数列{an}的公差为d,
∵a1+1,a2+1,a4+1成等比数列,∴ ![]() =(a1+1)(a4+1),
=(a1+1)(a4+1),
又S3=﹣15,∴ ![]() =﹣15,∴a2=﹣5.
=﹣15,∴a2=﹣5.
∴(﹣5+1)2=(﹣5﹣d+1)(﹣5+2d+1),解得d=0或d=﹣2.
d=0时,公比为1,舍去.
∴d=﹣2.
∴an=a2﹣2(n﹣2)=﹣5﹣2(n﹣2)=﹣2n﹣1
(2)解:由(1)可得:Sn= ![]() =﹣n2﹣2n.
=﹣n2﹣2n.
∴bn= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴数列{bn}的前n项和Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]()
=﹣ ![]()
=﹣ ![]() +
+ ![]()
【解析】(1)设等差数列{an}的公差为d,根据a1+1,a2+1,a4+1成等比数列,可得 ![]() =(a1+1)(a4+1),又S3=﹣15,可得
=(a1+1)(a4+1),又S3=﹣15,可得 ![]() =3a2=﹣15,解得a2 , 进而得到d.即可得出an . (2)由(1)可得:Sn=﹣n2﹣2n.可得bn=
=3a2=﹣15,解得a2 , 进而得到d.即可得出an . (2)由(1)可得:Sn=﹣n2﹣2n.可得bn= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,利用“裂项求和”即可得出.
,利用“裂项求和”即可得出.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:
分组 | 频数 | 频率 |
[60,70) | 10 | 0.1 |
[70,80) | 22 | 0.22 |
[80,90) | a | 0.38 |
[90,100] | 30 | c |
合计 | 100 | d |

(1)根据下面的频率分布表和频率分布直方图,求出a+d和b+c的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC.BC=2AD=4,EF=3,AE=BE=2,G为BC的中点. 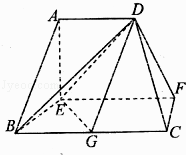
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p: ![]() <1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是( )
A.(﹣2,﹣1]
B.[﹣2,﹣1]
C.[﹣3,﹣1]
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点. 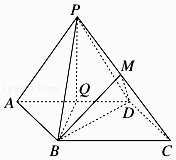
(1)求证:PA∥平面MBD;
(2)求二面角P﹣BD﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中,其中正确的个数为( ) ①命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2=0”;
②“ ![]() ”是“cos2α=0”的充分不必要条件;
”是“cos2α=0”的充分不必要条件;
③若命题 ![]() ,则p:x∈R,x2+x+1=0;
,则p:x∈R,x2+x+1=0;
④若p∧q为假,p∨q为真,则p,q有且仅有一个是真命题.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n和为Sn , 且 ![]() 是
是 ![]() 与(an+1)2的等比中项.
与(an+1)2的等比中项.
(1)求证:数列{an}是等差数列;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 求Tn .
,数列{bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱A1B1C1﹣A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为 . 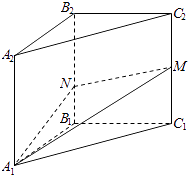
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com