练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    .设变量x,y满足约束条件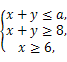且不等式x+2y≤14恒成立,则实数a的取值范围是　　　　. 


    [8,10]:不等式组表示的平面区域如图阴影部分所示,显然a≥8,否则可行域无意义.由图可知x+2y在点(6,a-6)处取得最大值2a-6,由2a-6≤14得,a≤10.

    ∴8≤a≤10.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如果关于x的不等式|x－a|＋|x＋4|≥1的解集是全体实数，则实数a的取值范围是

    A．(－∞，3]∪[5，＋∞)       B．[－5，－3]

    C．[3,5]                          D．(－∞，－5]∪[－3，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数y=a1-x(a>0,且a≠1)的图象恒过定点A,若点A在直线mx+ny-1=0(mn>0)上,则+的最小值为　　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设0≤α≤π,不等式8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,则α的取值范围为　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若实数x、y满足则z=的取值范围为(　)

    (A)(-∞,-4]∪[,+∞)   

    (B)(-∞,-2]∪[,+∞)

    (C)[-2,]  

    (D)[-4,]

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    咖啡馆配制两种饮料,甲种饮料每杯含奶粉9克、咖啡4克、糖3克,乙种饮料每杯含奶粉4克、咖啡5克、糖10克.已知每天原料的使用限额为奶粉3600克、咖啡2000克、糖3000克,甲种饮料每杯能获利润0.7元,乙种饮料每杯能获利润1.2元,每天应配制两种饮料各多少杯能获利最大?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正三角形ABC的顶点A(1,1)，B(1,3)，顶点C在第一象限，若点（x，y）在△ABC内部，则z=－x+y的取值范围是（   ）

    （A）(1－，2)     （B）(0，2)     （C）(－1，2)   （D）(0，1+)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知x＞0，y＞0，且2x＋y＝1，则＋的最小值为________；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为(　　)

    (A)6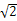  (B)4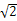  (C)6    (D)4

    查看答案和解析>>

    同步练习册答案