练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如果
    1+tanα
    1-tanα
    =2013    ，那么
    1
    cos2α
    +tan2α    =（　　）
    分析：利用二倍角的正切公式展开tan2α，展开二倍角的余弦公式，然后化弦为切，通分整理后即可得到答案．
    解答：解：∵
    1+tanα
    1-tanα
    =2013    ，
    ∴
    1
    cos2α
    +tan2α    =
    cos2α+sin2α
    cos2α-sin2α
    +
    2tanα
    1-tan2α
    =
    1+tan2α
    1-tan2α
    +
    2tanα
    1-tan2α

    =
    (1+tanα)2
    1-tan2α
    =
    1+tanα
    1-tanα
    =2013    ．
    故选：D．
    点评：本题考查了三角函数的化简与求值，考查了二倍角的正切和余弦公式，解答的关键是化弦为切，是中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2006•石景山区一模）已知函数y=f（x）对于任意θ≠
    kπ2
    （k∈Z），都有式子f（a-tanθ）=cotθ-1成立（其中a为常数）．
    （Ⅰ）求函数y=f（x）的解析式；
    （Ⅱ）利用函数y=f（x）构造一个数列，方法如下：
    对于给定的定义域中的x1，令x2=f（x1），x3=f（x2），…，xn=f（xn-1），…在上述构造过程中，如果xi（i=1，2，3，…）在定义域中，那么构造数列的过程继续下去；如果xi不在定义域中，那么构造数列的过程就停止．
    （ⅰ）如果可以用上述方法构造出一个常数列，求a的取值范围；
    （ⅱ）是否存在一个实数a，使得取定义域中的任一值作为x1，都可用上述方法构造出一个无穷数列{xn}？若存在，求出a的值；若不存在，请说明理由；
    （ⅲ）当a=1时，若x1=-1，求数列{xn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出五个命题：

    ①y=cos(x+)是奇函数；②如果f（x）=a·tanx+bcosx是偶函数，则a=0；③当x=2kπ+时，y=sin(x-)取得最大值；④y=sin的值域是［-1，1］；⑤点-，0是y=tan(2x+)的图象的一个对称中心．其中正确命题的序号是______________．

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修四1.4三角函数的图像与性质练习卷（一）（解析版） 题型：选择题

    如果sinα·tanα<0，且sinα＋cosα∈(0,1)，那么角α的终边在(　　)

    A．第一象限　   B．第二象限

    C．第三象限     D．第四象限

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏省南京市高三（上）期中数学模拟试卷（二）（解析版） 题型：解答题

    观察数列：
    ①1，-1，1，-1，…；
    ②正整数依次被4除所得余数构成的数列1，2，3，0，1，2，3，0，…；
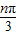    ③an=tan，n=1，2，3，…
    （1）对以上这些数列所共有的周期特征，请你类比周期函数的定义，为这类数列下一个周期数列的定义：对于数列{an}，如果______，对于一切正整数n都满足______成立，则称数列{an}是以T为周期的周期数列；
    （2）若数列{an}满足an+2=an+1-an，n∈N*，Sn为{an}的前n项和，且S2=2008，S3=2010，证明{an}为周期数列，并求S2008；
    （3）若数列{an}的首项a1=p，p∈[0，），且an+1=2an（1-an），n∈N*，判断数列{an}是否为周期数列，并证明你的结论．

    查看答案和解析>>

    同步练习册答案