
分析 (1)由椭圆的离心率公式,计算可得a与c的值,由椭圆的几何性质可得b的值,将a、b的值代入椭圆的方程计算可得答案;
(2)根据题意,设直线PQ的方程为y=k(x-3),联立直线与椭圆的方程可得(3k2+1)x2-18k2x+27k2-6=0,设出P、Q的坐标,由根与系数的关系的分析求出$\overrightarrow{MF}$、$\overrightarrow{FQ}$的坐标,由向量平行的坐标表示方法,分析可得证明;
(3)设直线PQ的方程为x=my+3,联立直线与椭圆的方程,分析有(m2+3)y2+6my+3=0,设P(x1,y1),Q(x2,y2),结合根与系数的关系分析用y1.y2表示出△FPQ的面积,分析可得答案.
解答 解:(1)由$\frac{{\sqrt{{a^2}-2}}}{a}=\frac{{\sqrt{6}}}{3}⇒a=\sqrt{6}$,
c=ea=$\frac{\sqrt{6}}{3}$×$\sqrt{6}$=2,
则b2=a2-c2=2,
∴椭圆E的方程是$\frac{x^2}{6}+\frac{y^2}{2}=1$.
(2)证明:由(1)可得A(3,0),设直线PQ的方程为y=k(x-3),
由方程组$\left\{\begin{array}{l}\frac{x^2}{6}+\frac{y^2}{2}=1\\ y=k({x-3})\end{array}\right.$,得(3k2+1)x2-18k2x+27k2-6=0,
依题意△=12(2-3k2)>0,得$-\frac{{\sqrt{6}}}{3}<k<\frac{{\sqrt{6}}}{3}$.
设P(x1,y1),Q(x2,y2),
则${x_1}+{x_2}=\frac{{18{k^2}}}{{3{k^2}+1}},{x_1}{x_2}=\frac{{27{k^2}-6}}{{3{k^2}+1}}$,
∵$F({2,0}),M({{x_1},-{y_1}}),\overrightarrow{MF}=({2-{x_1},{y_1}}),\overrightarrow{FQ}=({{x_2}-2,{y_2}})$,
由(2-x1)y2-(x2-2)y1=(2-x1)•k(x2-3)-(x2-2)•k(x1-3)=$k[{5({{x_1}+{x_2}})-2{x_1}{x_2}-12}]=k({5•\frac{{18{k^2}}}{{3{k^2}+1}}-2•\frac{{27{k^2}-6}}{{3{k^2}+1}}-12})=0$,
得$\overrightarrow{MF}∥\overrightarrow{FQ}$,∴M,F,Q三点共线.
(3)设直线PQ的方程为x=my+3.
由方程组$\left\{\begin{array}{l}\frac{x^2}{6}+\frac{y^2}{2}=1\\ x=my+3\end{array}\right.$,得(m2+3)y2+6my+3=0,
依题意△=36m2-12(m2+3)>0,得${m^2}>\frac{3}{2}$.
设P(x1,y1),Q(x2,y2),则${y_1}+{y_2}=-\frac{6m}{{{m^3}+3}},{y_1}{y_2}=\frac{3}{{{m^3}+3}}$.
∴${S_{△FPQ}}=\frac{1}{2}|{AF}|•|{{y_1}-{y_2}}|$=$\frac{1}{2}\sqrt{{{({{y_1}-{y_2}})}^2}}=\frac{1}{2}\sqrt{{{({{y_1}-{y_2}})}^2}-4{y_1}{y_2}}=\frac{1}{2}\sqrt{{{({-\frac{6m}{{{m^2}+3}}})}^2}-\frac{12}{{{m^2}+3}}}=\frac{1}{2}\sqrt{\frac{{12({2{m^2}-3})}}{{{{({{m^2}+3})}^2}}}}$,
令t=m2+3,则${S_{△FPQ}}=\frac{1}{2}|{{y_1}-{y_2}}|=\frac{1}{2}\sqrt{\frac{{12({2t-9})}}{t^2}}=\sqrt{3[{-9{{({\frac{1}{t}-\frac{1}{9}})}^2}+\frac{1}{9}}]}$,
∴$\frac{1}{t}=\frac{1}{9},t={m^2}+3=9$,即${m^2}=6,m=±\sqrt{6}$时,S△FPQ最大,
∴S△FPQ最大时直线PQ的方程为$x±\sqrt{6}y-3=0$.
点评 本题考查直线与椭圆的位置关系,涉及椭圆的几何性质,关键由离心率的公式求出椭圆的方程.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{5}{2},-2)$ | B. | $(-∞,-\frac{5}{2}]$ | C. | (-∞,-2] | D. | $[-\frac{5}{2},-2]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{5}{3}$x | B. | y=$\frac{3}{5}$x | C. | y=±$\frac{5}{3}$x | D. | y=±$\frac{3}{5}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},\frac{1}{4}})$ | B. | $({\frac{1}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{3}}}{4},0})$ | D. | $({0,\frac{{\sqrt{3}}}{4}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 条件 | 方程 |
| ①△ABC周长为10 | C1:y2=25 |
| ②△ABC面积为10 | C2:x2+y2=4(y≠0) |
| ③△ABC中,∠A=90° | C3:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) |
| A. | C3,C1,C2 | B. | C1,C2,C3 | C. | C3,C2,C1 | D. | C1,C3,C2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
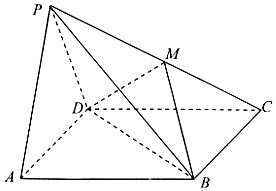 如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.
如图,四棱锥P-ABCD中,底面ABCD是矩形,平面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面MBD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com